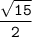Задача 1) Соединив центры О и М окружностей между собой и каждый из них с точкой касания, получим два треугольника с общей вершиной в точке А на отрезке между точками касания окружностей c прямой. Радиус, проведенный к касательной в точку касания, перпендикулярен ей ( свойство), Получившиеся прямоугольные треугольники подобны по равным вертикальным углам и накрестлежащим у их центров. Пусть радиус меньшей окружности будет r, а большей - R, и пусть часть отрезка между их точками касания у меньшей окружности будет х. Тогда отрезок у большей окружности 5-х ( см. рисунок) Тогда из подобия треугольников следует отношение: r:R=х:(5-х) 4:8=х:(5-х) 8х=20-4х 12х=20 х=5/3 - длина отрезка у меньшей окружности 5-5/3=10/3 длина отрезка у большей окружности По т.Пифагора ОА²=4²+(5/|3)² ОА²=16+25/9=169/9 ОА=13/3 Из треугольника в большей окружности МА²=8²+(10/3)²=676/9 МА=26/3 ОА+МА=13/3+26/3=39/3=13 ОМ=13 см ------- Задача 2 )Трапеция равнобедренная, следовательно, углы при основаниях равны. Т.к. диагональ делит трапецию на равнобедренные треугольники, то для острого угла она является биссектрисой (углы при ВД равны по свойству равнобедренной трапеции, и угол СВД равен половине угла СДА как накрестлежащий) Пусть угол СДВ=х Тогда угол ВАД=СДА=2х Угол АВД=ВАД=2х В треугольнике АВД сумма углов 2х+2х+х=180º х=36º 2х=72º Углы ВАД=СДА=72º
Задача 1) Соединив центры О и М окружностей между собой и каждый из них с точкой касания, получим два треугольника с общей вершиной в точке А на отрезке между точками касания окружностей c прямой. Радиус, проведенный к касательной в точку касания, перпендикулярен ей ( свойство), Получившиеся прямоугольные треугольники подобны по равным вертикальным углам и накрестлежащим у их центров. Пусть радиус меньшей окружности будет r, а большей - R, и пусть часть отрезка между их точками касания у меньшей окружности будет х. Тогда отрезок у большей окружности 5-х ( см. рисунок) Тогда из подобия треугольников следует отношение: r:R=х:(5-х) 4:8=х:(5-х) 8х=20-4х 12х=20 х=5/3 - длина отрезка у меньшей окружности 5-5/3=10/3 длина отрезка у большей окружности По т.Пифагора ОА²=4²+(5/|3)² ОА²=16+25/9=169/9 ОА=13/3 Из треугольника в большей окружности МА²=8²+(10/3)²=676/9 МА=26/3 ОА+МА=13/3+26/3=39/3=13 ОМ=13 см ------- Задача 2 )Трапеция равнобедренная, следовательно, углы при основаниях равны. Т.к. диагональ делит трапецию на равнобедренные треугольники, то для острого угла она является биссектрисой (углы при ВД равны по свойству равнобедренной трапеции, и угол СВД равен половине угла СДА как накрестлежащий) Пусть угол СДВ=х Тогда угол ВАД=СДА=2х Угол АВД=ВАД=2х В треугольнике АВД сумма углов 2х+2х+х=180º х=36º 2х=72º Углы ВАД=СДА=72º
Дано: AB=1; AC=√15; BM=MC; AM=2.
Найти: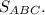
A₁ ∈ AM; AM=A₁M
ABA₁C - параллелограмм т.к. диагонали делятся точкой пересечения пополам (BM=MC по условию; AM=MA₁ по построению), поэтому A₁C=AB=1.
ΔAA₁C - прямоугольный т.к. выполняется теорема Пифагора:
AA₁² = (2AM)² = (2·2)² = 4² = 16;
AC²+CA₁² = (√15)²+1² = 15+1 = 16;
16 = 16 ⇒ AA₁² = AC²+CA₁².
Поэтому ∠ACA₁ = 90°, он лежит на против гипотенузы AA₁.
ABA₁C - прямоугольник т.к. это параллелограмма с углом в 90° (∠ACA₁=90°), поэтому ∠BAC=90°.
ответ: