(Комментарий забанен автором)
ответ 1/3
(НЕОБХОДИМЫЕ пояснения: Вершина пирамиды проектируется в центр вписаной окружности, r = H/3)
Ладно, может и правда, нужно...
Опускаем перпендикуляр из вершины на основание. То, что это будет центр правильного треугольника, и доказывать не надо - все так симметрично, что иначе и быть не может. Но, для фана, скажу, что раз ребра равны, то и проекции их на основание будут равны, а в правильном треугольнике центр описанной окружности совпадает с центром вписаной : Далее, проводим сечение пирамиды через ребро и высоту пирамиды. То, что это сечение пройдет через высоту противоположной грани (апофему), тоже доказать несложно, поскольку эта плоскость уже содержит 2 прямых, перпендикулярных ребру... Ну, и косинус двуграного угла равен расстоянию от центра треугольника до стороны, деленному на апофему. Ладно...
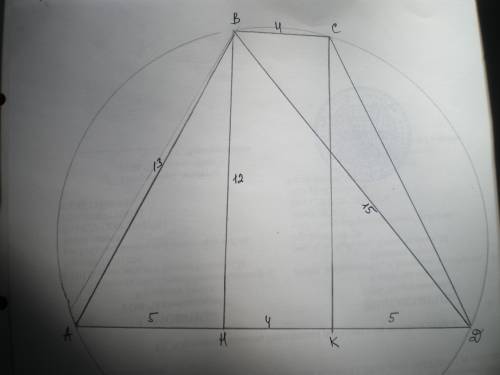
Трапеция АВСД является равнобедренной, т.к. окружность описать можно только вокруг равнобедренной трапеции. Значит, АВ=СД=13 см.
Проведем высоты ВН и СК. Тогда НК=ВС=4 см, АН=КД=(14-4):2=5 см.
Рассмотрим ΔАВН - прямоугольный. ВН=√(АВ²-АН²)=√(169-25)=√144=12 см.
Рассмотрим ΔАВД и найдем его площадь:
S=1\2 * АД * ВН= 1\2 * 14 * 12=84 см².
Из ΔВДН найдем ВД по теореме Пифагора ВД=√(ВН²+ДН²)=√(144+81)=√225=15 см
Найдем радиус окружности, описанной вокруг ΔАВД (этим же радиусом описана окружность вокруг трапеции АВСД)
R =(АВ*ВД*АД)/(4*S)=13*15*14\4*84=8,125 см
Найдем длину окружности по формуле С=2πR=2π*8,125=16,25π см
ответ: 16,25π см.
по вертикали 2 + зеркальное отражение
по горизонтали тоже самое