
Объяснение:
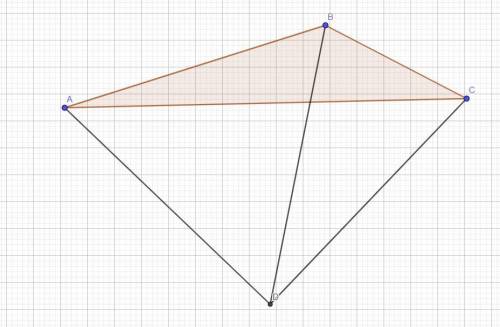
Пусть эта самая точка - D и пусть угол ABC все таки не тупой, тогда он не больше 90 градусов.
По условию AD = BD = DC, тогда треугольники BDC и ADB - равнобедренные, тогда угол DBC равен углу DCB, аналогично угол DBA равен углу DAB. Пусть угол DBC равен углу DCB равен x, а угол DBA равен углу DAB равен y. Тогда угол ABC по предположению не тупой, тогда x + y не больше 90. Заметим, что угол BAC меньше, чем BAD, тогда угол BAC < y, аналогично угол BCA меньше, чем угол BCD, значит угол BCA < x, но тогда сумма углов BAC и BCA меньше, чем x + y, а значит меньше 90 градусов. Но тогда в треугольнике ABC угол сумма углов меньше, чем 2x + 2y, но тогда она меньше 180, хотя должна быть равна 180. Противоречие, значит исходное предположение неверно и угол ABC - тупой. ч.т.д.
P.s. Небольшое пояснения почему угол BAC меньше, чем BAD и почему угол BCA меньше, чем угол BCD. Это так, потому что наша точка D по условию лежит вне треугольника, а значит отрезки AD и CD проходят за границами.
1) Пусть точка C - точка пересечения отрезков AB и MK.
Тогда по первому признаку равенства треугольников (две стороны и угол между ними) будут равными треугольники AKC и CBM.
А значит и углы тругольников AKС и СMB равны. Из этого следует, по теореме о параллельных прямых, так как накрест-лежащие углы (AKС и СMB) равны, то отрезки AK и MB параллельны.
2) См. рисунок.
Так как CH- биссектриса, то углы KCH и HCT равны между собой и равны половине угла KCP, т.е. 29°.
Так как CK и TH параллельны, то накрест-лежащие углы KCH и CHT равны, также 29°.
Угол CTH = 180 - HCT - CHT =180-29-29=122°.
Таким образом углы в треугольнике CHT: 29, 29, 122.
