S = 50 ед².
Объяснение:
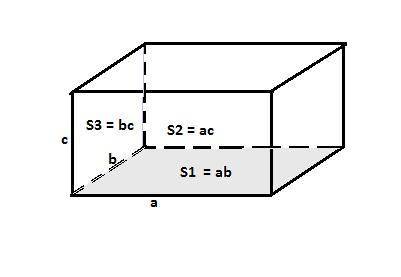
Пусть стороны прямоугольного параллелепипеда, образующие его измерения, равны "a", "b" и "c". Тогда площади основания и двух боковых граней равны
a·b = 48 (1), a·c = 40 (2) и b·c = 30 (3).
Выразим сторону b из равенств (1) и (3) и приравняем полученное:
b = 48/a и b = 30/c => 48/a = 30/c => c = 30a/48 = (5/8)a.
Подставим это значение в (2):
a·(5/8)a = 40 => a² = 320/5 = 64 => a = 8 ед.
Тогда из (1) b = 48/8 = 6 ед. c = 30/8 = 5 ед. (из 2).
Найдем по Пифагору диагональ основания:
d = √(a²+b²) = √(64+36) = 10 ед.
Площадь диагонального сечения равна:
S = d·c = 10·5 = 50 ед².
A1. Две прямые на плоскости называются параллельными, если они:
4) не пересекаются
А2. Один из признаков параллельности двух прямых гласит:
Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны
А3. Выберите утверждение, являющееся аксиомой параллельных прямых:
Через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной
А4. Если две параллельные прямые пересечены секущей, то:
Соответственные углы равны
А5. Если прямая перпендикулярна одной из двух параллельных прямых, то:
Она перпендикулярна и другой
А6. Всякая теорема состоит из нескольких частей:
Условия и заключения
А7. При пересечении двух прямых секущей образуются углы, имеющие специальные названия:
Накрест лежащие, соответственные, односторонние
А8. Аксиома – это:
Положение геометрии, не требующее доказательства
А9. Выберите утверждение, которое является признаком параллельности прямых:
Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны
А10. Если прямая не пересекает одну из двух параллельных прямых, то:
Другую прямую она тоже не пересекает
или
С другой прямой она совпадает
1)P=20см, следовательно a=5 см
2)угол A=60градусов => угол C=60 градусов, а из этого => угол D = углу B = (360-60*2)/2=120 градусов
3)если провести диагонали, то ромб разобьется на 4 больших треугольника:
нам нужны верхний (ABD) и нижний(DBC)-они равностороннии, т.к. каждый угол=60 градусов => DB= 5 см