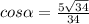
Объяснение:
Дано: Окр.OR-описанная
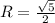
ΔАВС - прямоугольный
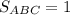
ВК и СМ - медианы
Найти: cosα
1. Окр. OR - описана около ΔАВС ⇒СВ - диаметр (прямой угол опирается на диаметр)

2. Рассмотрим ΔАВС - прямоугольный.
Пусть меньший катет = a, больший - b.
Тогда:
Площадь треугольника:
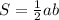
По теореме Пифагора:
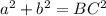
Составим систему:
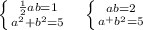
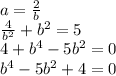
По теореме Виета:

Или
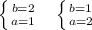
Тогда АС=1; АВ=2.
3. Рассмотрим ΔАВК - прямоугольный.
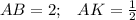 (ВК-медиана)
(ВК-медиана)
По т. Пифагора
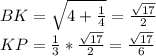 (св-во пересекающихся медиан)
(св-во пересекающихся медиан)
4. Рассмотрим Δ МАС - прямоугольный.
 (СМ-медиана)
(СМ-медиана)
По т. Пифагора
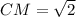
 (св-во пересекающихся медиан)
(св-во пересекающихся медиан)
5. Рассмотрим ΔКРС

Используем теорему косинусов:
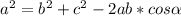
Имеем
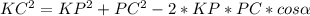

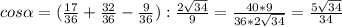

ответ: 40cm
Объяснение:
Пусть трапеция ABCD . Большее основание это AD=45 см.
боковые стороны АВ =20см, CD=15cm.
Пусть точка пересечения биссетрисс Т , и по условию задачи Т принадлежит основанию ВС.
Заметим что ∡TAD=∡ATB (накрест лежащие). Но ∡BAT=∡TAD, так как АТ - биссетриса.
Отсюда следует, что ∡BAT=∡BTA => ΔABT - равнобедренный.
То есть АВ=ВТ=20см.
По той же причине и треугольник СТD тоже равнобедренный,
ТС=CD=15 cm
Тогда ВС=ВТ+СТ=20+15=35 см
Тогда средняя линия трапеции MN=(AD+BC)/2=(45+35)/2= 40 cm
без рисунка объяснить не могу но там ответ 60 градусов будет