Несмотря на то, что прямоугольный треугольник, сторонами которого являются высота, медиана и отрезок гипотенузы между ними, является Пифагоровым (8, 15,17), и высота делит гипотенузу, длина которой равна 17*2 = 34, на отрезки длиной 17 - 8 = 9 и 17 + 8 = 25 (как и положено, 9*25 = 15^2), сам треугольник не является целочисленным, и его катеты надо просто вычислить по теореме Пифагора.
Меньший катет равен √(9^2 + 15^2) = 3*√34;
Больший катет равен √(25^2 + 15^2) = 5*√34;
Ну да, еще периметр 34 + 8*√34 ;
Объяснение:
Прямую, проходящую через середину отрезка перпендикулярно к нему, называют серединным перпендикуляром к отрезку.
Свойства серединных перпендикуляров треугольника
Каждая точка серединного перпендикуляра к отрезку равноудалена от концов этого отрезка. Верно и обратное утверждение: каждая точка, равноудаленная от концов отрезка, лежит на серединном перпендикуляре к нему.
Точка пересечения серединных перпендикуляров, проведенных к сторонам треугольника, является центром окружности, описанной около этого
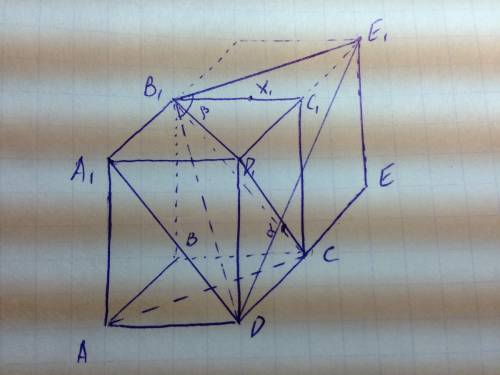
чтобы построить такой угол, нужно построить прямые, параллельные рассматриваемым прямым и лежащие в одной плоскости)))
применить удобнее теорему косинусов...
ответ на третий вопрос: ДА.
Крайние положения для точки Х1 -- это точки В1 и С1
и значение косинуса 30 градусов лежит между косинусами углов A1OD1
(О -- точка пересечения диагоналей основания), A1C1D1
(в первой четверти косинус убывает с увеличением угла...
если точка Х1 движется от точки С1 к В1,
рассматриваемый угол увеличивается)))