Средняя линия треугольника соединяет середины двух сторон, параллельна третьей стороне и равна ее половине.
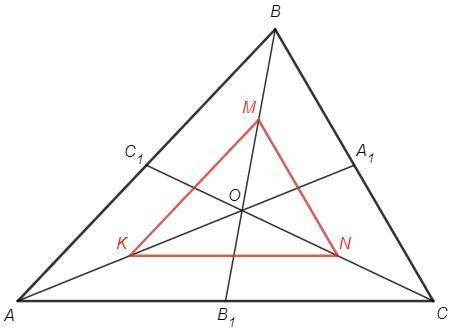
Отрезки KM, MN, KN являются средними линиями в треугольниках AOB, BOC, AOC.
a) KM||AB, MN||BC, KN||AC
KMN~ABC по трем параллельным сторонам
б) KM=AB/2, MN=BC/2, KN=AC/2
P(ABC) =2P(KMN) =44*2 =88 (см)
в) Отношение соответствующих отрезков (медиан, биссектрис, высот и любых отрезков, построенных сходным образом) в подобных треугольниках равно коэффициенту подобия.
k=AB/KM =2
Медианы ABC вдвое больше медиан KMN.
А F Е Д
ЕД=ЕС=4см (т.к. в треугольникеЕСД уголЕСД=90-45=45градусов => треугольник равнобедренный)
СЕ=ВF=4см (т.к. высоты)
уголАВF=90-60=30градусов
АF=2АВ, т.к. катет АF лежит против угла 30градусов, значит равен половине гипотенузы АВ.
Пусть АF=х, тогда АВ=2х.
4^2+х^2=(2х)^2
16+х^2=4х^2
3х^2=16
х^2=16/3
х=4/(корень из3)
АД=4/(корень из3) + 3 + 4 = (4/корень из3) +7
S=1/2 * ((4/корень из3) +7 +3) * 4 = ((4/корень из3) + 10) * 2 = 20+(8/корень из3)