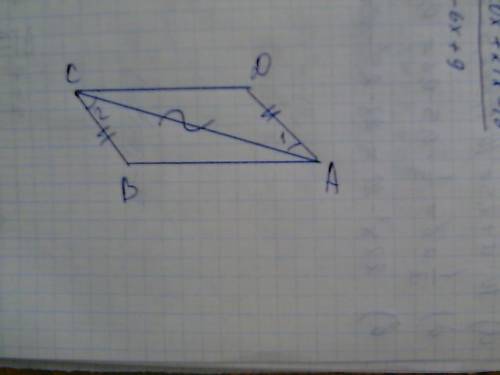
Вся "трудность" тут в том, что диагональ делит параллелограмм на 2 прямоугольных треугольника - это потому, что для них просто выполняется теорема Пифагора. Ну, или, если хотите, проекция большей стороны на меньшую равна этой меньшей стороне:
11*(7/11) = 7;
То есть окружности вписаны в прямоугольные треугольники, "приставленные" друг к другу катетами. Пусть a - эта диагональ, перпендикулярная стороне b = 7 (точнее - обеим сторонам, равным 7), при этом сторона параллелограмма с = 11 играет роль гипотенузы в каждом из этих треугольников.
r = (a + b - c)/2;
и линия, соединяющая центры обеих вписанных окружностей, проходит через середину катета (диагонали) а. Тангенс искомого угла между этой линией и этой диагональю (я обозначаю его α)
tg(α) = r/(a/2 - r) = a/(c - b) - 1 = √((c+ b)/(c - b)) - 1;
(я просто подставил выражение для r и a = √(c^2 - b^2) );
tg(α) = √((11+ 7)/(11 - 7)) - 1 = √(18/4) - 1 = (3/2)√2 - 1; это ответ.
Я считал, что речь идет о диагонали тупого угла. Между прочим, условие можно трактовать и так, что речь идет о диагонали острого угла. Уточняйте :)
а) Параллельные прямые АА1, ВВ1, ММ1 вместе с пересекающим их отрезком АВ образуют плоскость, которая пересекает плоскость альфа - только по прямой! А1, В1, М1 - лежат на одной прямой.
б) Используя теорему Фалеса, делаем вывод, что В1М1 = А1М1.
Значит ММ1 - средняя линия в трапеции АА1В1В. Пусть АА1 = х
Тогда по свойству средней линии:
ММ1 = (ВВ1 + х)/2
8 = (12+х)/2
х = 16-12 = 4 см.
ответ: 4 см.