ДАНО: Равносторонний треугольник. Р = 6 см - периметр.
НАЙТИ: высоту треугольника.
РЕШЕНИЕ: Рисунок задаче и решение - в приложении.
Применены два метода:
1) геометрия и теорема Пифагора
2) тригонометрические функции.
ОТВЕТ: Высота b = √3 см (≈ 1,73)

Треугольник с прямым углом - это прямоугольный треугольник.
Так как меньшие стороны "прилегают" к прямому углу, то эти стороны - катеты.
Так как катеты имеют длины 6 см и 8 см, то также такой треугольник - египетский (треугольник с соотношением сторон, равным 3:4:5). Следовательно, гипотенуза равна 10 см (можно также проверить через теорему Пифагора).
Высота, проведённая к большей стороне - высота, проведённая к гипотенузе (так как гипотенуза - самая большая сторона в прямоугольном треугольнике).
Высота, проведённая к гипотенузе равна произведению катетов, делённому на гипотенузу.
То есть -
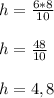
h = 4,8 см.
ответ: 4,8 см.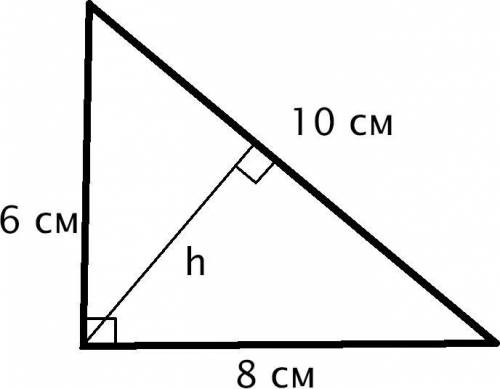
Дано: ΔАВС - равносторонний, Р=6 см. ВН - высота. Найти ВН.
Решение: АВ=ВС=АС=6:3=2 см.
Рассмотрим ΔАВН - прямоугольный и найдем ВН по теореме Пифагора: ВН=√(АВ²-АН²)=√(2²-1²)=√(4-1)=√3 см.
ответ: √3 см.