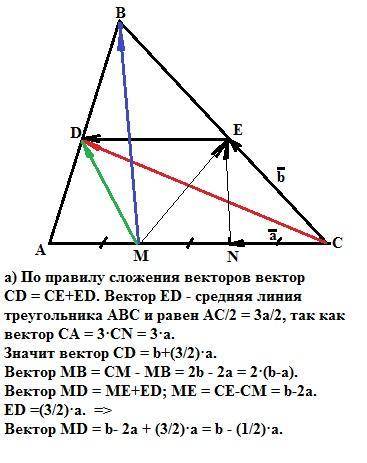
а) CD= b+(3/2)·a. MB= 2·(b-a). MD= b- (1/2)·a.
б) доказательство в объяснении.
Объяснение:
a) По правилу сложения векторов вектор CD = CE+ED. Вектор ED - средняя линия треугольника АВС и равен АС/2 = 3а/2, так как вектор СА = 3·СN = 3·a. Значит вектор CD = b+(3/2)·a.
Вектор МВ = СМ - MB = 2b - 2a = 2·(b-a).
Вектор MD = ME+ED; ME = CE-CM = b-2a. ED =(3/2)·a. =>
Вектор MD = b- 2a + (3/2)·a = b - (1/2)·a.
б) Вектор NE = b-a. Вектор МВ = 2·(b-a). Следовательно, вектор NE СОНАПРАВЛЕН вектору МВ, то есть, параллелен ему, что и требовалось доказать.
УголДСО=СОА, как внутрение разностороние углы при сечной, отсюда треугольник СОА-равнобедренный, а значит сторона СА=АО.
х-коефициент пропорцыональночти.
АО=АС=3х, ОК=х, отсюда АК=АО+ОК=3х+х=4х. Известно, что у паралелограмма все паралельные стороны равны, так, как его периметр становит 28см., то имеем уравнение:
3х+4х+3х+4х=28
14х=28
х=2см.
Значит АК=4х=4*2=8см.
ответ:8см.