40дм²
Объяснение:
Пусть будет
а- диагональ ромба
б- диагональ ромба
c- сторона ромба
h- высота.
S1=12 dm²
S2=16dm²
Диагоналное сечение это прямоугольник, со сторонами диагональ ромба и высота. Площадь диагонального сечения произведение высоты на диагональ ромба.
S1=ah, выразим диагональ а
а=S1/h
a=12/h
S2=бh, выразим диагональ б
б=S2/h
б=16/h
Диагонали ромба делятся пополам, образуя прямоугольные треугольники.
Разделим каждую диагональ пополам.
12/h:2=12/h*1/2=6/h дм половина диагонали ромба
16/h:2=16/h*1/2=8/h дм половина диагонали ромба
По теореме Пифагора найдем сторону ромба.
с²=(6/h)²+(8/h)²=36/h²+64/h²=100/h² dm
c=√(100/h²)=10/h dm
Все стороны ромба равны между собой. Найдем периметр ромба.
Р=4*с=4*10/h=40/h dm
Площадь боковой поверхности призмы равна произведению периметра основания на высоту
Sбок=Р*h=40/h*h=40 dm²
ответ: АВ=8см
Объяснение: высота АМ делит ∆АВС на 2 прямоугольных треугольника АВМ и АМС. Рассмотрим полученный ∆АМС. В нём АМ и МС- катеты, а АС - гипотенуза. Найдём АМ по теореме Пифагора:
АМ²=АС²-МС²=7²-1²=49-1=48; АМ=√48см.
Рассмотрим полученный ∆АВМ. В нём ВМ и АМ- катеты, а АВ- гипотенуза, угол В=60°, и так как сумма острых углов прямоугольного треугольника составляет 90°, то угол ВАМ=90-60=30°. Катет лежащий напротив него равен половине гипотенузы поэтому ВМ=АВ÷2. Пусть ВМ=х, тогда АВ=2х. Составим уравнение используя теорему Пифагора:
АВ²-ВМ²=АМ²
(2х)²-х²=(√48)²
4х²-х²=48
3х²=48
х²=16
х=√16=4
Итак: ВМ=4см, тогда АВ=4×2=8см
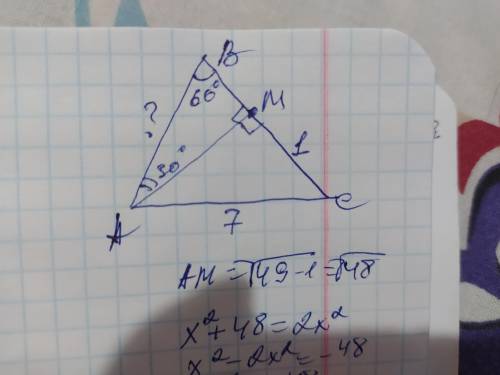
Если треугольник равнобедренный то медиана является и бисектрисо и высотой
Тогда АМ=МС=24:2=12,треугольник ВМС- прямоугольный,т.к ВМ - высота
Высоту ВМ найдем за теоремой Пифагора
37²=12²+х²
пусть ВМ=х
х²=37²-12²
х²=(37-12)*(37+12)-по формуле
х=√1225
х=35
Итак,Медиана ВМ=35 см
ответ:35 см