Сторона вписанного в окружность правильного треугольника равна 6 . найдите его площадь

👇

Ответ:

NurGangsta

17.08.2021

Нужно вспомнить: Все углы в таком треугольнике равны 60 градусов
Медианы в точке их пересечения делятся в соотношении 2/1 (считая от вершины угла)
Медиана в правильном треугольнике=высоте=биссектрисе
Катет прямоугольного треугольника, противолежащий углу 30 градусов, равен половине гипотенузы.
Отсюда - высота треугольника = R +1/2R =1,5R = 9

Если принять катет, противолежащий половине угла треугольника (30 градусов) за х
то сторона треугольника будет 2х
По формуле Пифагора (2х) ² = х² + 9²
4х² = х²+81
3х² = 81
х² = 27
х= 3√3
2х=6√3
Итак, известна высота 9, известна сторона треугольника 6√3 .
Площадь треугольника равна половине произведения его высоты на основание.
Считайте, это уже просто сделать
3 года назад

4,4(37 оценок)

Ответ:

irajuta82

17.08.2021

Т.к. треугольник правильный, то все его стороны равны, т.е. в данном случае они все равны 6, а все углы правильного треугольника = 60 градусов
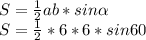
$S=\frac{1}{2}ab*sin \alpha \\ S=\frac{1}{2}*6*6*sin60$
S=18*√3/2=9√3

4,4(6 оценок)

Открыть все ответы

Ответ:

Malvina1903

17.08.2021

1.
т.к. вектор_m _|_ вектор_n ---> соs(вектор_m_и_вектор_n) = 0
mx*nx + my*ny = 0 (знаменатель не может быть=0)
(ax + 2bx)(5ax -4bx) + (ay + 2by)(5ay - 4by) = 0
5(ax)² + 6ax*bx - 8(bx)² + 5(ay)² + 6ay*by - 8(by)² = 0
5((ax)²+(ay)²) + 6(ax*bx+ay*by) - 8((bx)²+(by)²) = 0
5 + 6(ax*bx+ay*by) - 8 = 0
6(ax*bx+ay*by) = 3
ax*bx+ay*by =1/2
соs(вектор_a_и_вектор_b) = ax*bx + ay*by = 1/2
угол между векторами = 60° (знаменатель для косинуса =1))
использовано: скалярный квадрат вектора=квадрату его длины)))
(ax)²+(ay)² = |a|² = 1
(bx)²+(by)² = |b|² = 1
2.
т.к. вектор_e1 _|_ вектор_e2 ---> соs(вектор_e1_и_вектор_e2) = 0
e1x*e2x + e1y*e2y = 0 (знаменатель не может быть=0)
найдем |AB| = √(AB²x + AB²y) =
= √((4e1x + 4e2x)² + (4e1y + 4e2y)²) =
= √(16((e1x)² + 2e1x*e2x + (e2x)² + (e1y)² + 2e1y*e2y + (e2y)²)) =
= 4√(1+1+2*0) = 4√2
|AC| = √(AC²x + AC²y) = √((2e1x + 6e2x)² + (2e1y + 6e2y)²) =
= √(4((e1x)² + 6e1x*e2x + (3e2x)² + (e1y)² + 6e1y*e2y + (3e2y)²)) =
= 2√(1+9+6*0) = 2√10
соs(векторAB_и_векторAC) =
= ((4e1x+4e2x)(2e1x+6e2x) + (4e1y+4e2y)(2e1y+6e2y)) / (8√20) =
= (8(e1x)²+32e1x*e2x+24(e2x)²+8(e1y)²+32e1y*e2y+24(e2y)²) / (16√5)
= (8+24+0) / (16√5) = 2 / √5
BC = √(16*2 + 4*10 - 2*8√20*2 / √5) = √(72-64) = √8 = 2√2
AC² = 40 = AB² + BC² = 32+8
т.е. треугольник АВС прямоугольный, но не равнобедренный...
ответ похоже не отсюда))) или неточность в задании векторов)))
чтобы получился угол 45° векторАС должен быть коллинеарен е2

(везде над буквами стоят векторы) 1.даны векторы m=a+2b и n=5a-4b m⊥n. | a| =| b| =1. найти угол меж

(везде над буквами стоят векторы) 1.даны векторы m=a+2b и n=5a-4b m⊥n. | a| =| b| =1. найти угол меж

4,8(58 оценок)

Ответ:

arusy

17.08.2021

Дано: угол ВАС = 40 град.

АD - ,биссектриса

АВ = АС = AD

Найти угол ВDC.

1) Достроим отрезки ВD и СD так, чтобы получились треугольники ABD и ACD.

2) Поскольку АD - биссектриса (по условию), то угол BAD = углу CAD = 20 градусам.

3) Треугольники BAD и CAD равны по второму признаку равенства треугольников, так как АD - общая сторона, стороны АВ и АС равны (по условию), и углы BAD и CAD равны (по второму пункту моего решения)

4) Треугольник BAD - равнобедренный, так как AB = AD (по условию). Аналогично с треугольником CAD.

5) Так как по свойству равнобедренных треугольников углы при основании равнобедренного треугольника равны, а сумма всех углов треугольника равна 180 градусам, составляем уравнение, где у - неизвестный угол.

2у + 20 = 180

у = 80

Аналогично с треугольником CAD

6) Так как угол BDA = 80 градусам, и угол CDA = 80 градусам (по 5 пункту моего решения), то по аксиоме о сумме градусных мер угол BDC = BDA + CDA, то есть

BDC = 80 + 80 = 160.

ответ угол BDC = 160 градусам. Ч.Т.Н.

4,8(24 оценок)

Это интересно:

Дом-и-сад

29.12.2020

Как покрасить стены поверх обоев: лучшие способы...

Здоровье

21.06.2021

Как распознать симптомы японского энцефалита?...

Хобби-и-рукоделие

14.10.2022