
15°, 150° и 15°
Объяснение:
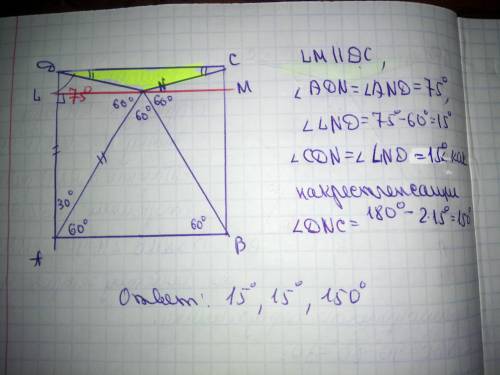
Треугольник ABN - равносторонний, т.е. AB=AN=BN
Но ABCD - квадрат => AB=AN=BN=BC=CD=AD
Рассмотрим треугольник ADN:
<A=90°-<BAN = 90°-60° =30°
AD=AN => треугольник ADN - равносторонний
Значит, <ADN=<AND=(180°-30°)/2 = 75°
Рассмотрим треугольник BCN:
<B=90°-<ABN = 90°-60° =30°
BC=BN => треугольник BCN - равносторонний
Значит, <BNC=<BCN=(180°-30°)/2 = 75°
Рассмотрим треугольник DNC:
<CDN = 90°-<ADN = 90°-75° = 15°
<DCN = 90°-<BCN = 90°-75° = 15°
<DNC = 360° -<AND-<ANB-<BNC = 360°-75°-60°-75° = 150°


90=12h
h=7.5 (см)