Площадь прямоугольника равна произведению его двух смежных сторон
S=ab
из уменьшением в n раз одной из его сторон его площадь уменьшается в n раз
из увеличением в n раз одной из его сторон его площадь увеличивается в n раз
если одну его сторону увеличить в 4 раза, а другую- уменьшить в 8 раз (так как уменьшали в большее число раз чем увеличивали), то площадь уменьшится в 8/4=2 раза
или с формул
новая площадь будет равна
S'=(4a)(b/8)=(ab)/2, откуда
2S=S' или S'=S/2
т.е. после указанных в условии преобразований площадь прямоугольника уменьшится в 2 раза
Пусть дано ΔАВС i ΔА 1 В 1 С 1 причем АС = А 1 С 1 , ВМ i B 1 M 1 - медианы, ВМ = B 1 M 1 , ∟BMC = ∟B 1 M 1 C 1 .
Докажем, что ΔАВС = Δ А 1 В 1 С 1 .
Рассмотрим ΔВМС i ΔB 1 M 1 C 1 .
1) ВМ = B 1 M 1 (по условию)
2) ∟BMC = ∟В 1 М 1 С 1 (по условию)
3) МС = М 1 С 1 (половины равных стopiн AC i A 1 С 1 ).
Итак, ΔВМС = ΔВ1М1С1 за I признаку.
Рассмотрим ΔАВС i Δ А 1 В 1 С 1 .
1) AC = А 1 С 1 (по условию)
2) ∟C = ∟C 1 (т. К. ΔВМС = Δ B 1 M 1 C 1 )
3) ВС = В 1 С 1 (т. К. ΔВМС = Δ B 1 M 1 C 1 ).
Итак, ΔАВС = ΔА 1 В 1 С 1 , за I признаку.
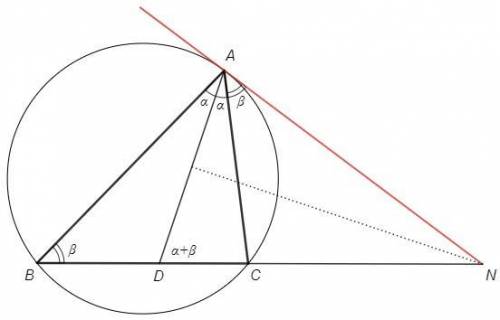
Точка N лежит на серединном перпендикуляре к AD, следовательно равноудалена от концов отрезка.
△AND - равнобедренный, DAN=ADN
DAN =A/2 +NAC
ADN =A/2 +B (внешний угол △BAD)
=> NAC =B =∪AC/2
Угол между прямой NA и хордой AC равен половине дуги, стягиваемой хордой, следовательно NA является касательной.
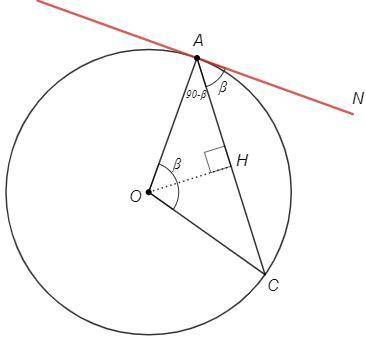
Докажем этот признак для острого угла NAC.
NAC =∪AC/2 =AOC/2 =AOH
△AOC - равнобедренный, OH - биссектриса и высота
OAH =90-AOH =90-NAC => OAN =OAH+NAC =90
Прямая NA перпендикулярна радиусу OA, следовательно является касательной.
Для тупого угла как для смежного с NAC:
180-NAC =(360-∪AC)/2 => NAC=∪AC/2, далее по доказанному.
уменьшится в 2 раза допустим та скорона которая увеличилась в 4 раза = 1 а другая 8
1*8=8
а после условия
4*1=4