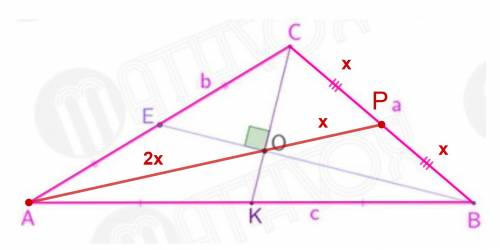
1) Проведем медиану AP, ⇒ CP = PB.
2) AO:OP = 2:1 (по свойству пересекаемых медиан)
3) ΔCOB — прямоугольный, т.к. CO⊥BO (CO∈CK, BO∈BE, CK⊥BE по условия задачи)
4) OP — медиана ΔCOB, т.к. ΔCOB — прямоугольный, CP = PB, а медиана делит сторону, на которую опущена, только в прямоугольном треугольнике, и эта сторона — гипотенуза, а угол, с которого проведена медиана — прямой.
Следовательно, OP = 1/2CB, или OP:CB = 1:2
5) AP:CB = (AO+OP):CB = (2+1):2 = 3:2.
ответ: отношение третьей медианы к соответствующий стороне — 3:2.
1) Проведем медиану AP, ⇒ CP = PB.
2) AO:OP = 2:1 (по свойству пересекаемых медиан)
3) ΔCOB — прямоугольный, т.к. CO⊥BO (CO∈CK, BO∈BE, CK⊥BE по условия задачи)
4) OP — медиана ΔCOB, т.к. ΔCOB — прямоугольный, CP = PB, а медиана делит сторону, на которую опущена, только в прямоугольном треугольнике, и эта сторона — гипотенуза, а угол, с которого проведена медиана — прямой.
Следовательно, OP = 1/2CB, или OP:CB = 1:2
5) AP:CB = (AO+OP):CB = (2+1):2 = 3:2.
ответ: отношение третьей медианы к соответствующий стороне — 3:2.

Применим теорему Фалеса:
Если на одной стороне угла отложить какие-либо отрезки, через их концы провести параллельные прямые, то отношение отрезков на одной стороне угла будет равно отношению отрезков на другой стороне⇒
BK:KM=BP:PD=10:9 и CM:AM=CD:DP=1:1, так как AM - медиана
Пусть BP=10x; PD=DC=9x⇒BC=28x
BK=10y;KM=9y⇒BM=19y
Обозначим угол CBM=α⇒
Smbc=1/2*BM*BC*sinα=1/2*19y*28x*sinα=14*19xysinα=266xysinα
Skbp=1/2*BK*BP*sinα=1/2*10x*10y*sinα=50xysinα⇒
Skpcm=Smbc-skbp=266xysinα-50xysinα=216xysinα
Медиана делит тр-ник на 2 равновеликих тр-ка⇒
Sabc=2Smbc=2*266xysinα=532xysinα⇒
Skpmc:Sabc=216xysinα:532xysinα=216:532=54:133
ответ: 54:133