Question

Катеты прямоугольного треугольника равны 3 и 4 соответственно. найдите высоту треугольника, проведенную к гипотенузе.

Answer 1

Объяснение:

Рисунок прилагается.

Гипотенуза АВ = √(АС^2 + ВС^2) = √(3^2 + 4^2) = √(9+16) = √25 = 5.

Угол sin A = BC/AB = 4/5 = 0,8

Высота CD = h = AC*sin A = 3*0,8 = 2,4

Answer 2

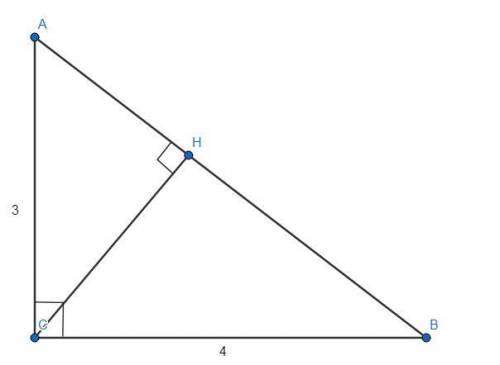
Дано:

ΔABC - прямоугольный.

∠С = 90°.

АС = 3.

ВС = 4.

СН - высота.

Найти:

СН = ?

По теореме Пифагора :

$BC^{2} +AC^{2} = AB^{2} \\4^{2} +3^{2} = AB^{2}\\16+9 = AB^{2}\\ AB^{2}=25\\AB = 5$

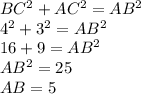
Высота прямоугольного треугольника, проведённая к гипотенузе, равна произведению катетов делённому на гипотенузу (это утверждение не сложно доказать с метода площадей).

Тогда :

$CH = \frac{AC*BC}{AB} \\CH = \frac{3*4}{5} \\CH = 2,4$

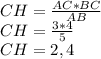
ответ: 2,4.