Площадь боковой поверхности пирамиды равна половине произведения апофемы на периметр основания.
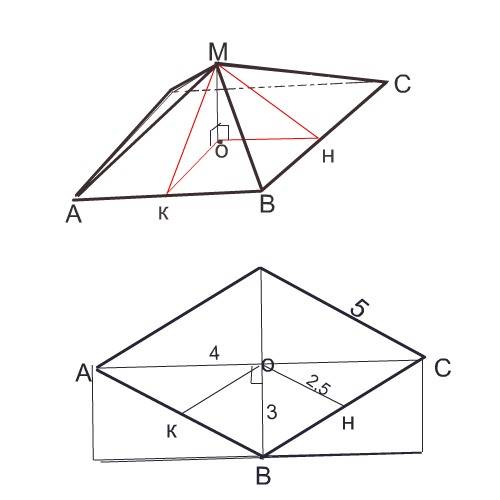
Начертив отдельно основание пирамиды, заметим, что диагонали делят ромб на 4 "египетских" треугольника, отношение сторон в которых равно 3:4:5. Следовательно, сторона ромба равна 5 см.
Площадь каждой грани равна половине произведения апофемы на сторону ромба.
Апофему найдем из треугольника ОМН = ОМК
Если высота пирамиды равна 1 см, то
МН=√(2,5²+1²)=√7,25 см
S бок.=1/2* 4*5√7,25 =10 √7,25 см² или 50√0,29 см²
Медианы треугольника пересекаются в одной точке. Эта точка делит каждую медиану в отношении 2:1 (считая от вершины).
Медианы в правильном треугольнике равны.
R =10см - 2 части - отрезок от точки пересечения медиан до вершины
Вся медиана - 15см
ответ: 15 см
1)Рассмотрим ΔМКЕ-прямоугольный(по построению, угол КЕМ=90)
Т.к. угол МКЕ=45, то угол КМЕ=90-45=45 ⇒ ΔМКЕ-равнобедренный⇒ катеты КЕ=МЕ=14
КЕ-искомая проекция
ответ: 14