1. Каждая сторона треугольника составлена из 2 таких отрезков. Поэтому их длины будут 3+4 = 7, 3+5 = 8 и 4+5 = 9... это обычный остроугольный треугольник без особых примет. Уж точно не прямоугольный.
2. Дуга АСВ равна 150 градусам, а дуга АМВ - 210 градусов. Угол АМВ опирается на дугу АСВ, то есть равен 150/2 = 75 градусов, угол АВМ = 90 градусов - АМ диаметр, угол АСВ = 210/2 = 105 градусов (независимо от положения точки С).
3. пусть CE = 3*x; ED = 4*x; CD = 7*x;
(3*x)*(4*x) = 3*36; x = 3;
CD = 21; наименьшее значение радиуса - если АВ еще "влезает" в окружность, то есть 39/2 = 19,5
4. Половина основания 6, площадь 48, периметр 32, r = 2*S/P = 3;
R = 10*10*12/(4*S) = 25/4;
4 пункт подробнее с чертежом и другим решением
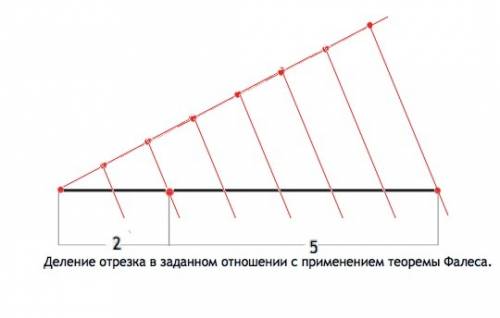
Для решения применим теорему Фалеса: Если на одной из двух прямых отложить последовательно несколько отрезков и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой пропорциональные отрезки.
Чтобы без линейки с делениями разделить отрезок, длина которого не известна, нужно от одного из концов этого отрезка провести под углом к нему вс луч и на этом луче на равном расстоянии отметить нужное количество точек.
а) На вс луче отложим через равные промежутки 2+5 =7 точек. Затем через последнюю точку и конец заданного отрезка проведём прямую и через все точки ещё 6 прямых, параллельных ей. При этом заданный отрезок будет разделен на 7 равных частей. Отсчитаем 2 из получившихся отрезков. Остальная часть равна 5 отмеренным отрезкам, а исходный разделен в отношении 2:5
Можно на заданном отрезке откладывать не 7 отрезков, а провести всего 2 прямые - через седьмую и параллельно ей через вторую точку. Заданный отрезок будет разделён в нужном отношении.
б) и в) делим точно так же.
180°-54°=126° значение второго угла