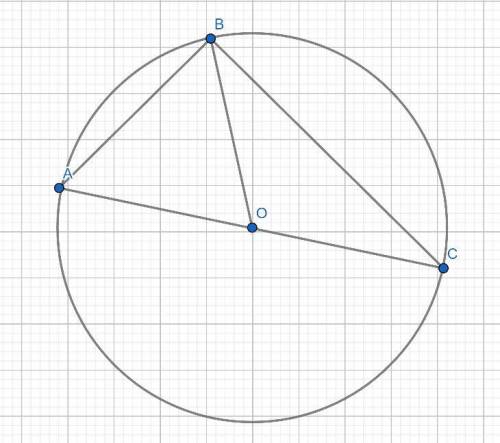
Дан прямоугольный ΔABC с прямым углом B. BO - медиана, проведенная из вершины прямого угла. Опишем около ΔABC окружность. Тогда гипотенуза AC будет являться диаметром окружности, так как вписанный угол ABC является прямым, то он опирается на диаметр окружности.
Медиана в треугольнике является отрезком, опущенным из вершины треугольника на середину противолежащей стороны. BO делит AC пополам. BO соединяет точку на окружности и центр окружности - тч.О, т.е. является радиусом окружности.
Отрезки BO = AO = OC - являются радиусами одной и той же окружности. ⇒ BO = AC/2.
векторы а и b пртивоположно-направлены, значит
a=-k*b , где k>0 - действительное число
(|a|=k*|b|)
модуль вектора а равен: |a|=корень((-6)^2+4^2+12^2)=корень (196)=14
14=k*28
k=14/38=0.5
b=-1/k *a=-1/0.5*{-6,4,12}=-2{-6,4,12}=*{-2*(-6),-2*4,-2*12}={12,-8,-24}