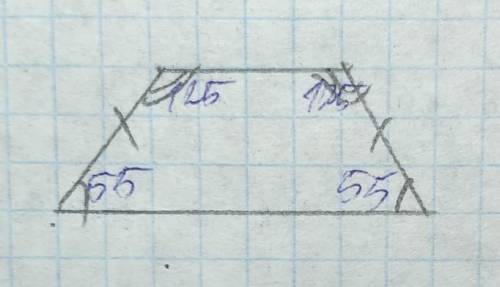
55;55;125;125
Объяснение:
смотри на фото)
Равнобедренная трапеция имеет равные углы у нижнего основания(нижний левый и нижний правый углы равны) и равные углы у верхнего основания(верхний левый и верхний правый тоже равны).
Если один из углов равен 55°, то он имеет рядом ещё один такой угол. Сумма углов четырехугольника равна 360°, два угла по 55° в сумме дают 110°,
360-110=250°, это приходится на оставшиеся два равных угла, а так как они равны,
250:2=125°, это градусная мера двух нижних углов.
Надеюсь понятно объяснил) Если можно, сделай мой ответ лучшим.
Объяснение:
1)Найти координаты конца вектора а ⃖(-2; 1; 3), если его начало совпадает с точкой А(5; 4; -1).
В(5+(-2) ; 4+1 ;-1+3) или В(3;5;2).
2)Даны координаты точек А(-3; 2; -1), В(2; -1; -3), С(1; -4; 3), Д(-1; 2; -2). Найти длину вектора 2(АВ) ⃖+ 3(СД) ⃖.
Вектор АВ(5;-3;-2) , тогда вектор 2АВ (10;-6;-4) ;
Вектор СД(-2 ;6;-5) ,тогда вектор 3СД (-6;18;-15);
Вектор 2АВ+3СД (10+(-6);-6+18;-4+(-15) ) или (4;12;-19)
3)При каком значении а векторы АВ и СД коллинеарны, если
А(-2; -1; 2), В(4; -3; 6), С(-1; а-1; 1), Д(-4; -1; а).
Вектор АВ (6;-2;4) , вектор СД(-3;-1-а+1 ;а-1) или СД(-3; -а ;а-1)
Вектора коллинеарны, если соответствующие координаты пропорциональны :
6:(-3)=-2:(-а)=4:(а-1) ( можно взять любые две части),
6:(-3)=-2:(-а) или -6а=6 или а=-1.
4)Если вектор а ̅(1; 2п + 1; -2) перпендикулярен вектору в ̅(п; 1; 2п), то п равно?
Для перпендикулярности двух ненулевых векторов необходимо чтобы их скалярное произведение равнялось нулю :
1*n+(2n+1)*1+(-2)*2n=0,
n+2n+1-4n=0, -n=-1, n=1.
После того, как согнули прямоугольник, опустим высоты BF и DE на линию сгиба - диагональ АС. По формуле для высоты из прямого угла треугольника на его гипотенузу имеем: BF=DE= AB*DC/AC =20*15/25 = 12см. Прямоугольнык треугольники АDE и BFC равны.
По Пифагору находим АЕ=FC = √(15²-12²) = 9см.
Тогда EF= АС-AE-FC =25-18=7cм.
В прямоугольном тр-ке DEF по Пифагору найдем DF=√(12²+7²)=√193см.
Из прямоугольного треугольника DBF по Пифагору найдем искомое расстояние BD = √(DF²+BF²) =√(193+144) = √337см ≈ 18,36см.
P.S Арифметику хорошо бы еще раз проверить...