Sокр = πr² = π· а²Sin²α/(4·(1+Sin(α/2))²).
Объяснение:
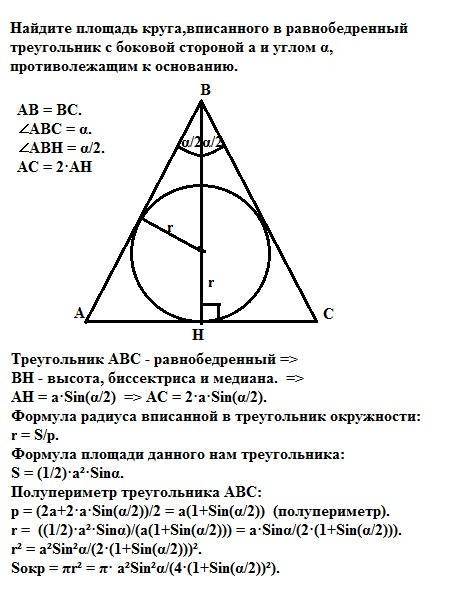
Треугольник АВС - равнобедренный =>
ВН - высота, биссектриса и медиана. =>
AH = a·Sin(α/2) => AC = 2·a·Sin(α/2).
Формула радиуса вписанной в треугольник окружности:
r = S/p.
Формула площади данного нам треугольника:
S = (1/2)·a²·Sinα.
Полупериметр треугольника АВС:
p = (2a+2·a·Sin(α/2))/2 = а(1+Sin(α/2)).
r = ((1/2)·a²·Sinα)/(а(1+Sin(α/2))) = a·Sinα/(2·(1+Sin(α/2))).
r² = а²Sin²α/(2·(1+Sin(α/2)))².
Sокр = πr² = π· а²Sin²α/(4·(1+Sin(α/2))²).
Sокр = πr² = π· а²Sin²α/(4·(1+Sin(α/2))²).
Объяснение:
Треугольник АВС - равнобедренный =>
ВН - высота, биссектриса и медиана. =>
AH = a·Sin(α/2) => AC = 2·a·Sin(α/2).
Формула радиуса вписанной в треугольник окружности:
r = S/p.
Формула площади данного нам треугольника:
S = (1/2)·a²·Sinα.
Полупериметр треугольника АВС:
p = (2a+2·a·Sin(α/2))/2 = а(1+Sin(α/2)).
r = ((1/2)·a²·Sinα)/(а(1+Sin(α/2))) = a·Sinα/(2·(1+Sin(α/2))).
r² = а²Sin²α/(2·(1+Sin(α/2)))².
Sокр = πr² = π· а²Sin²α/(4·(1+Sin(α/2))²).

2. ВС=2АВ=6,5*2=13 см
АВ=1/3*3,6 дм=1/3*36 см=12 см,
следовательно, опять же по 1 пункту
ВС=2*АВ=2*12=24 см
ответ: катет равен 12 см
гипотенуза равна 24 см, меньший катет равен 12 см