a)Треугольник АВМ - равнобедренный ⇒ АВ=ВМ
Треугольник ДМС - равнобедренный ⇒ СД=МС
А так как АВ=СД (как противоположные стороны параллелограмма), то и ВМ=МС.
Значит, если АВ=х, то ВС=2х.
Полупериметр равен 36:2=18 см.
х+2х=18
3х=18
х=6
АВ=СД=6 см
ВС=АД=2·6=12 (см)
ответ. 6 см и 12 см.
b)Проведем высоты ВМ и СН. Так, как меньшая основа будет 6см., а большая 12, и эта трапецыя равобедренная, то ВС=МН, отсюда АМ=НД, ВС=12-6=6см.
НД+АМ=12-6=6см., а значит НД=6/2=3см.
Расмотрим треугольник АВМ, у него: ВМА=90гр., как угол при высоте; ВАМ=60гр., за условием задачи, отсюда угол АВМ=30гр. Значит АМ=1/2*ВА, отсюда ВА=2*АМ=2*3=6см.
ответ:6см.
Расстояние равно √433,0625 ≈ 20,8 см.
Объяснение:
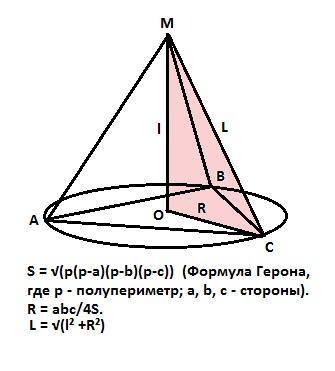
Соединим точку М с вершинами данного треугольника. Получится пирамида, вершина которой проецируется в центр описанной вокруг треугольника окружности, так как если наклонные (расстояния от М до вершин) равны, то равны и их проекции (радиус описанной окружности).
Найдем площадь данного нам треугольника по формуле Герона, где р - полупериметр треугольника, a,b,c - его стороны:
S = √(p(p-a)(p-b)(p-c)) = √(42·16·14·12) = 336cм².
Формула радиуса описанной окружности:
R = a·b·c/4·S = 26·28·30/(4·336) = 16,25см.
Искомое расстояние находим по Пифагору:
L= √(МО²+R²) =√(13²+16,25²) = √433,0625 ≈ 20,8 cм.
2)(√3/2)²*(1/2)²-(1/2)²+(√2/2)²+(√2/2)²=3/4*1/4-1/4+1/2+1/2=15/16
3)1/2+1/2=1