Відповідь:
Пояснення:
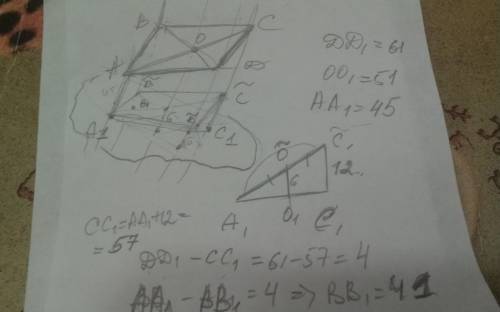
Пусть О-точка пересечения диагоналей
А1, В1, С1, Д1, О1 проекции соответствующих вершин и точки пересечения на плоскость
Пусть АА1=45; ДД1=61 и ОО1=51
Сделаем паралельний перенос паралепипеда таким образом, чтоби одна вершина, с наименьшим растоянием к плоскости, ледала на плоскости А1
Тогда рассмотрим △А1С~С1, прямая О~О1 - средняя линия етого △, так как при любой проекции сохраняются соотношение паралельних прямих, → С~С1=2О~О1
О~О1=ОО1-АА1=6 → С~С1=12 → СС1=АА1+12=57
Так как АВ||СД → С~Д~||А1В~ → ДД1-СС1=4
АА1-ВВ1=4→ ВВ1=45-4=41
Відповідь:
Пояснення:
Пусть О-точка пересечения диагоналей
А1, В1, С1, Д1, О1 проекции соответствующих вершин и точки пересечения на плоскость
Пусть АА1=45; ДД1=61 и ОО1=51
Сделаем паралельний перенос паралепипеда таким образом, чтоби одна вершина, с наименьшим растоянием к плоскости, ледала на плоскости А1
Тогда рассмотрим △А1С~С1, прямая О~О1 - средняя линия етого △, так как при любой проекции сохраняются соотношение паралельних прямих, → С~С1=2О~О1
О~О1=ОО1-АА1=6 → С~С1=12 → СС1=АА1+12=57
Так как АВ||СД → С~Д~||А1В~ → ДД1-СС1=4
АА1-ВВ1=4→ ВВ1=45-4=41

Радиус вписанной в прямоугольной треугольник окружности равен r=(a+b-c)\2
Радиус описанной вокруг прямоугольного треугольника окружности равен R=c\2
где a, b-катеты, c - гипотенуза
отсюда с=2*5=10
a+b=2*2+10=14
По теореме Пифагора a^2+b^2=c^2
a^2+b^2=10^2=100
a^2+b^2=(a+b)^2-2ab=100
14^2-2ab=100
2ab=196-100=96
ab=96:2=48
a+b=14
ab=48
(6+8=14; 6*8=48)
по теореме обратной к теореме Виета
a=6 b=8 или a=8, b=6
ответ: длины катетов 6 и 8