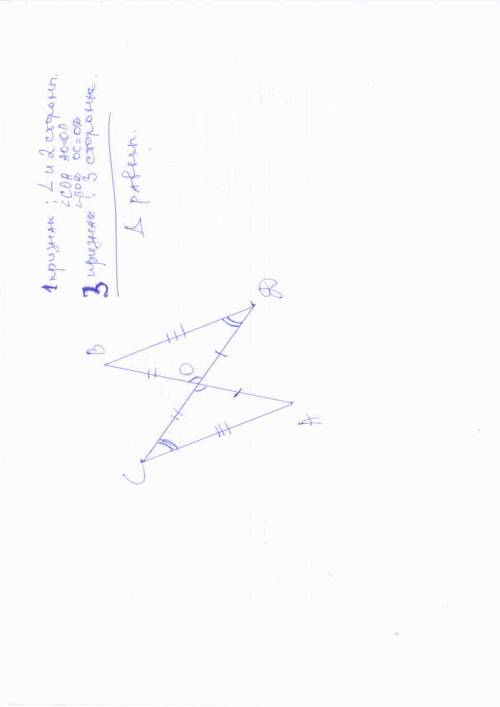
Пусть H - середина ABCD, MH - высота пирамиды MABCD,
MH - медиана, биссектриса и высоты треугольника DBM => H - середина DB=> HL - средняя линия треугольника DMB => 2LH=DH;
AH перпендикулярно BD ( как диагонали квадрата),
AH перпендикулярно МH ( т.к. МH - высота пирамиды)
DB пересекает MH в точке H => AH перпендикулярна плоскости DMB, значит угол HLA = 60° (по условию),
CA = √(CB^2+AB^2)=6√2 (по теореме Пифагора)
HA=1/2CA=3√2
LM=AH/tg60° = √6
DM=2LM=2√6
MH=√(DM^2-DH^2)=√6 (по теореме Пифагора)
ответ: √6
ABCDA1B1C1D1 - правильная призма, ABCD - квадрат в основании.
AC - диагональ квадрата. Треугольник ACD прямоугольный. CD=DA = 2 корня из 2.
По т.Пифагора AC = 4 см.
Треугольник AEC - равнобедренный прямоугольный (AE=EC, угол Е прямой).
Площадь равнобедренного тр-ка:
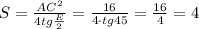
DO - перпендикуляр из точки D к диагонали AC. Значит, DO - половина диагонали BD. Диагонали квадрата равны, значит DO = AC/2 = 2 см.
Тругольник ODE прямоугольный. Угол DOE = 60 гр. Из определения котангенса
ctg(DOE) = OD/DE
DE = OD/ctg(DOE) = 2 корня из 3.
E - середина ребра DD1.
Значит DD1 = 2*DE = 4 корня из 3.