Точка А Точка В Точка С
x y z x y z x y z
1 2 -3 -2 0 4 -1 -2 1
а) Вектор АВ Вектор ВС Вектор АС
x y z x y z x y z
-3 -2 7 1 -2 -3 -2 -4 4
Модуль √62 ≈7,8740 Модуль √14 ≈3,74166 Модуль √36 =6
б) Середины сторон:
Точка А Точка В Точка С
1 2 -3 -2 0 4 -1 -2 1
АВ/2 = ((1-2)/2;(2+0)/2; (-3+4)/2) = (-0,5; 1; 0,5),
ВС/2 = ((-2-1)/2; (0-2)/2; (4+1))/2) = (-1,5; -1; 2,5),
АС/2 = ((1-1)/2; (2-2)/2;(-3+1)/2) = (0; 0; -1).
в) Площадь по формуле Герона.
Периметр Р Полупер. р p - a p - b p - c
17,61567 8,8078 0,9338 5,06618 2,8078
S =10,816654 .
По векторному произведению АВ(-3; -2; 7) на АС(-2; -4; 4)
i j k| i j
-3 -2 7| -3; -2
-2 -4 4| -2 -4 = -8i -14j + 12k + 12j + 28i - 4k = 20i - 2j + 8k.
S = (1/2)*√(400 + 4 + 64) = (1/2)*√468 = (1/2)*6√13 = 3√13 ≈ 10,816654.
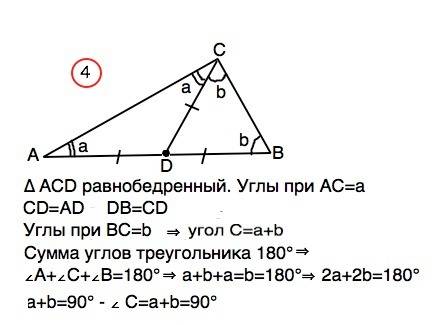
4) Примем угол А=а, угол В=b
В равнобедренном треугольнике углы при основании равны. ⇒
в ∆ АДС ∠АCD=∠CAD=а.
По условию СD=АD, а СD - медиана, и АD=ВD, ⇒ СD=ВD.
∆ ВDС равнобедренный. Углы при основании равнобедренного треугольника равны. ∠ВСD=∠СВD=b
Из найденного следует: угол С=а+b
Сумма углов треугольника 180°
Угол А+угол С+угол В=180° ⇒
а+b+a+b=180°
2a+2b=180°⇒
a+b=90° - угол С=а+b=90°
(Полезно помнить: Если в треугольнике медиана равна половине стороны, к которой проведена, этот треугольник – прямоугольный).
======
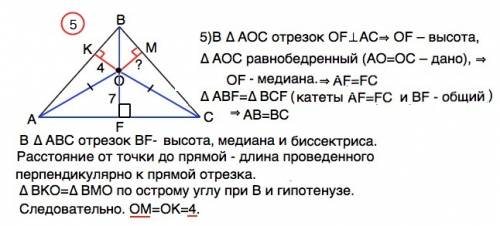
5) В ∆ АОС отрезок ОF перпендикулярен АС⇒ ОF – высота, а т.к. ∆ АОС равнобедренный (АО=ОС – дано), то ОF - медиана. ∆ АВF=∆ BCF– они прямоугольные с равными катетами: АF=FC (доказано), и ВF - общий, ⇒ АВ=ВС.
В равнобедренном ∆ АВС отрезок ВF- не только высота, но и медиана и биссектриса. Расстояние от точки до прямой - длина проведенного перпендикулярно к прямой отрезка.
Треугольники ВКО и ВМО прямоугольные с общей гипотенузой ВО и равным острым углом при В. Эти треугольники равны по углу и гипотенузе. Следовательно. ОМ=ОК=4.
≈≈≈≈≈≈≈≈
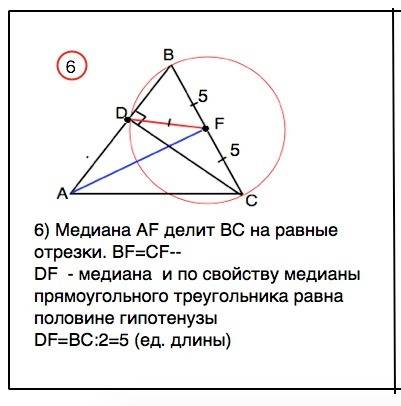
6) Медиана AF делит ВС на равные отрезки. BF=CF⇒
DF - медиана ∆ BDC и по свойству медианы прямоугольного треугольника равна половине гипотенузы
DF=ВС:2=5 (ед. длины)
======
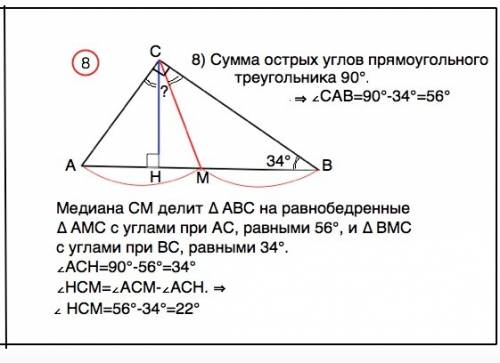
8) Сумма острых углов прямоугольного треугольника 90°. ⇒
угол САВ=90°-34°=56°
Медиана СМ делит ∆ АВС на равнобедренные: ∆ АМС с углами при АС, равными 56°, и ∆ ВМС с углами при ВС, равными 34°.
Угол АСН=90°-56°=34°
∠НСМ=∠АСМ -∠АСН.
Угол НСМ=56°-34°=22°