Написала на картинке.
1. Каждая сторона треугольника меньше суммы двух других сторон. Пользуясь этой теоремой, пишем неравенства для сторон шестиугольника.
2. Неравенство для второго вопроса -
PK+KL+LM+MN+NR+PR < PA+KA+DK+DL+LB+BM+ME+EN+NC+RC+PF+FR.
3. Неравенство для третьего вопроса -
2*(PK+KL+LM+MN+NR+PR) < PA+KA+DK+DL+LB+BM+ME+EN+NC+RC+PF+FR+(PK+KL+LM+MN+NR+PR).
4. На картинке.
5. Пользуемся ответами от 3 и 4 задания. Сумма периметров треугольников АВС и DEF равна 12 см (7 см+5 см). Я не знаю, там нужно писать единицы измерения или нет.
Вот такое неравенство в итоге получилось -
2*(PK+KL+LM+MN+NR+PR) < 12 см.
6. Логично, что поделить на 2.
Получаем, что -
2*(PK+KL+LM+MN+NR+PR) < 12 см
PK+KL+LM+MN+NR+PR < 6 см.
Это нам и нужно было доказать.



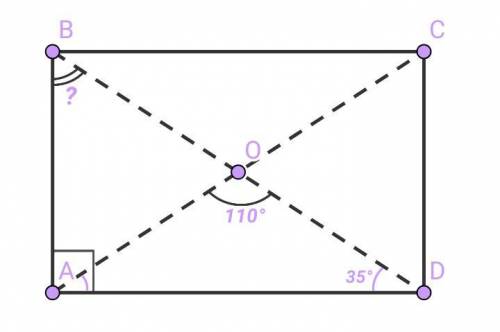
Дано :
Четырёхугольник ABCD —прямоугольник.
Отрезки АС и BD — диагонали.
Точка О — точка пересечения диагоналей.
Угол AOD = 110°.
Найти :
Угол ABD = ?
Рассмотрим треугольник AOD.
Диагонали прямоугольника точкой пересечения делятся пополам и равны.
Следовательно —
АО = OD.
Тогда треугольник AOD — равнобедренный.
У равнобедренного треугольника углы у основания равны.
Следовательно —
Угол OAD = угол ODA.
По теореме о сумме углов треугольника —
Угол ODA = 0,5*(180° - угол AOD) = 0,5*(180° - 110°) = 0,5*70° = 35°.
Рассмотрим треугольник BAD — прямоугольный (так как угол BAD = 90° по определению прямоугольника).
Сумма острых углов прямоугольного треугольника равна 90°.
Следовательно —
Угол ABD = 90° - угол BDA
Угол ABD = 90° - 35° = 55°.
55°.
Опустим вторую высоту, она разделит большее основание на два отрезка, один из которых равен меньшему основанию.
рассмотрим два прямоугольных треугольника:
1- катет 12см, гипотенуза 15см, второй катет, равный меньшему основанию, находим по т.Пифагора. корень квадратный из 15*15-12*12=81 или 9см
2 - катет 12см и гипотенуза 13см, второй катет корень квадратный из 13*13-12*12=25 или 5см.
Большее основание 5+9=14см