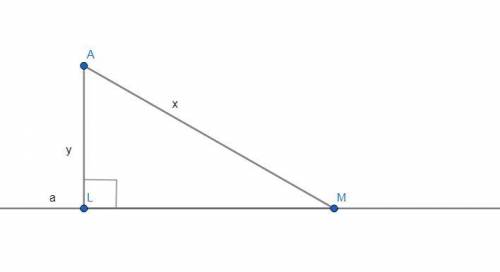
Чертёж смотрите во вложении.
Дано:
а - прямая.
АL - перпендикуляр от точки А до прямой а.
АМ - наклонная от точки А до прямой а.
∠ALM = 90°.
АМ+AL = 11 см.
Разность длин наклонной и перпендикуляра = 1 см.
Найти:
Расстояние от точки А до прямой а = ?
О каком расстоянии идёт речь в задании? Дело в том, что расстояние от точки до прямой - длина перпендикуляра, проведённого из этой точки к этой прямой. Поэтому, мы будем искать длину перпендикуляра AL.Так как АМ - наклонная, то она больше перпендикуляра AL (это не сложно доказать, если рассмотреть получившиеся прямоугольный ΔALM). Итак, поэтому, AM-AL = 1 см.Введём переменные. Пусть АМ = х, а AL = y. Составим систему линейных уравнений и решим её методом подстановки -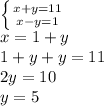
AL = y = 5 см.ответ: 5 см.
1) Так как угол MNO = 60°, а стороны MO=ON как радиусы, то треугольник MNO - равнобедренный и углы OMN и MNO равны друг другу (60°)
В сумме эти углы дают 120°, значит третий угол MON будет равен 180°-120° = 60°. Значит треугольник MON - разносторонний и сторона MN равна радиусу. Диаметр равен двум радиусам:
D=2R=2MN=2*5,4=10,8см
2) Угол MNR равен сумме углов MNO и ONR , то есть: 60° + 90° = 150°
3) Аналогично рассмотрим треугольник OKL , так как KL = MN , то точно так же треугольник OKL является равносторонним, а значит все его углы равны по 60° => угол OKL = углу NKL = 60°
ответ:V170
Объяснение:
|AB|=V(под конем) (-6-3)^2+(0-5)^2+(7+1)^2=V81+25+64=V170