1.
P(4;3), T(-2;5).
Используем уравнение прямой, проходящей через две точки.
Если даны две точки A(x₁; y₁) и B(x₂; y₂), тогда уравнение прямой, проходящей через эти две точки будет
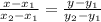
То есть у нас даны две точки P(4;3) и T(-2;5), уравнение прямой, проходящей через них будет

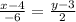
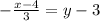
-(x-4) = 3·(y-3),
4 - x = 3y - 9,
3y + x - 9 - 4 = 0,
x + 3y - 13 = 0.
Можно сделать проверку: подставим координаты каждой точки в уравнение и проверим выполнение равенства.
P(4;3):
4 + 3·3 - 13 = 4 + 9 - 13 = 0. Верно.
T(-2;5):
(-2) + 3·5 - 13 = -2 + 15 - 13 = 0. Верно.
ответ. x + 3y - 13 = 0.
2.
x + 3y - 13 = 0,
Уравнение оси Ox (оси абсцисс): y = 0. Подставим это в уравнение прямой и получим x + 3·0 - 13 = 0, ⇔ x = 13.
Итак, пересечение прямой с осью Ox дает точку (13;0).
Уравнение оси Oy (оси ординат): x = 0. Подставим это в уравнение прямой и получим 0 + 3y - 13 = 0, ⇔ 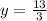 .
.
Итак, пересечение прямой с осью Oy в точке 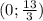 .
.
3.
Дана прямая x - y + 2 = 0 и окружность (x-2)² + (y-1)² = 9.
Чтобы найти координаты точек пересечения решим систему двух уравнений на два неизвестных.
Из уравнения прямой находим y = x+2, подставим это в уравнение окружности: (x-2)² + ( x+2 - 1)² = 9,
(x-2)² + (x+1)² = 9,
x² - 4x + 4 + x² + 2x + 1 = 9,
2x² - 2x + 5 - 9 = 0,
2x² - 2x - 4 = 0,
x² - x - 2 = 0,
D = (-1)² - 4·1·(-2) = 1 + 8 = 9 = 3²,
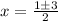
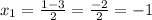
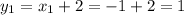
Итак, координаты первой точки (-1; 1).
 .
.
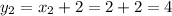
Итак, координаты второй точки (2; 4).
ответ. (-1; 1), (2; 4).
а) Рассмотрим основание:
расстояние стороны ВС от диаметра равно к = √(8²-(12/2)²) = √64-36) =√28 = 2√7.
расстояние от точки А до стороны ВС равно 8-2√7.
В сечении будет прямоугольник с основанием 8-2√7 и высотой 24 (по высоте цилиндра и призмы.
б) Угол между заданными плоскостями α = arc tg ( 8-2√7)/24 =
arc tg 0.112854 = 0.112379 радиан = 6.438818 градусов