R≅5,04
H≅5,04
Объяснение:
Объём цилиндра :
(1) V = πR²H,
где R - радиус цилиндра, H - высота цилиндра.
Площадь полной поверхности цилиндра:
(2) S = πR² + 2πRH
Выразим из формулы (1) высоту цилиндра и подставим значение в формулу (2):
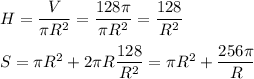
Найдём минимум этой функции по переменной R. Для этого вычислим производную и определим критические точки.
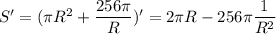 .
.
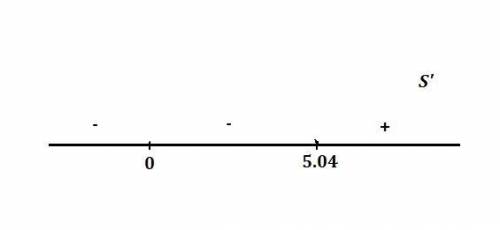
S' = 0,
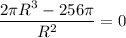
Если R = 0, то производная не существует.
![2\pi (R^3-128)=0\\\\R^3 = 128\\\\R=\sqrt[3]{128}](/tpl/images/2088/5757/d960d.png)
R≅ 5.04
Отметим эти значения на координатной прямой и oпределим знак производной на трёх полученных числовых интервалах. (Cм.рис)
Известно, что в точке минимумa производная меняет знак с минусa на плюс. Соответственно, наименьшее количество материала можно получить, если радиус основания цилиндра R=5,04
Вычислим соответствующую высоту цилиндра:
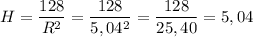
1.
V = 96π см³
Sбок = 60π см²
2.
V = 54√2π см³
Sбок = 36π см²
Объяснение:
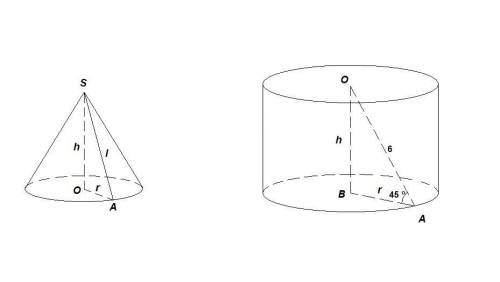
1.
r = 6 см, h = 8 см.
Из прямоугольного треугольника SOA по теореме Пифагора найдем образующую:
l = √(r² + h²) = √(36 + 64) = √100 = 10 см
V = 1/3 πr²h, где
r - радиус основания,
h - высота.
V = 1/3 π · 6² · 8 = 1/3 π · 36 · 8 = 96π см³
Sбок = πrl, где
r - радиус основания,
l - образующая.
Sбок = π · 6 · 10 = 60π см²
2.
ОА = 6 см
ΔОАВ прямоугольный равнобедренный (∠ОАВ = 45°), значит
r = h
По теореме Пифагора:
r² + h² = OA²
2r² = 36
r² = 18
r = 3√2 см
h = r = 3√2 см
V = πr²h
V = π · 18 · 3√2 = 54√2π см³
Sбок = 2πrh
Sбок = 2 · π · 3√2 · 3√2 = 36π см²
(х-2)/(-4-2)=(у+3)/(1+3)
(х-2)/(-6)=(у+3)/4
2(х-2)=-3(у+3)
2х-4+3у+9=0
2х+3у+5=0 - уравнение прямой АВ
Если точка С лежит на прямой АВ, то ее координаты должны удовлетворять уравнению:
2*1+3*(-1)+9=0
8≠0 - точки не лежат на одной прямой.
|АВ|=√(2+4)²+(-3-1)²=√(36+16)=√52=2√13
|AC|=√(2-1)²+(-3+1)²=√(1+4)=√5
|BC|=√(-4-1)²+(1+1)²=√(25+4)=√29
Наибольшая сторона 2√13≈7,21
√5+√29≈7,62≠2√13