Признаки и свойства параллельных прямых

Question

Геометрия: Признаки и свойства параллельных прямых

olenkazyateva · Accepted Answer

По определению трапеции её основания параллельны: BC||AD .

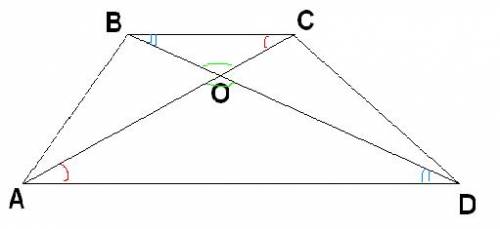
Рассмотрим треугольники BOC и DOA:

1) Угол BCO равен углу OAD ( как накрест лежащие при пересечении параллельных прямых BC и AD секущей AC )

2) Угол CBO равен углу ODA ( как накрест лежащие при пересечении параллельных прямых BC и AD секущей BD )

Следовательно, треугольники BOC и DOA подобны.

Отношение площадей подобных треугольников равно квадрату коэффициента подобия.

k (коэф. подобия) равен отношению сходственных сторон подобных треугольников =>

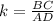
$k=\frac{BC}{AD}$

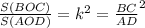
$\frac{S(BOC)}{S(AOD)}=k^2= \frac{BC}{AD} ^2$