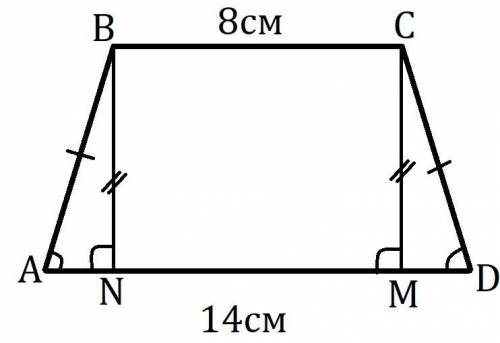
Дана трапеция ABCD, BC║AD, AB=CD, BC=8см, AD=14см, S(ABCD)=44см².
Найти P(ABCD).
Пусть CM⊥AD, BN⊥AD и M,N∈AD.
Площадь трапеции равна произведению средней линии и высоты опущенной на основание.
S(ABCD) =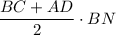 
= BN·(8см+14см):2 = BN·11см = 44см²
BN = 44:11 см = 4см
ΔABN = ΔDCM по гипотенузе и острому углу (AB=DC и ∠BAN=∠CDM т.к. трапеция равнобедренная), поэтому AN=MD
NBCM - прямоугольник, поэтому NM=BC=8см
AN = (AD-NM):2 = (14см-8см):2 = 3см
В прямоугольном ΔABN (∠N=90°): BN=4см и AN=3см, по Египетскому треугольнику AB=5см.
CD=AB=5см
P(ABCD) = AB+BC+CD+AD = 5см+8см+5см+14см = 32см
ответ: 32см.
Возьмем прямоуг. тр-к, гипотенуза которого = 55, а один из катетов = 44, то другой катет по т. Пифагора = √55^2-44^2=33
из (1) найдем основание тр-ка = 33*2=66
(2)Биссектриса внутреннего угла треугольника делит противоположную сторону в отношении, равном отношению двух прилежащих сторон
возьмем один из отрезков, на которые делит биссектриса угла, за х, то другой будет = 55-х
из (2) составим соотношение:
х/55=(55-х)/66
66х=55(55-х)
х=25
другой отрезок будет = 55-25=30