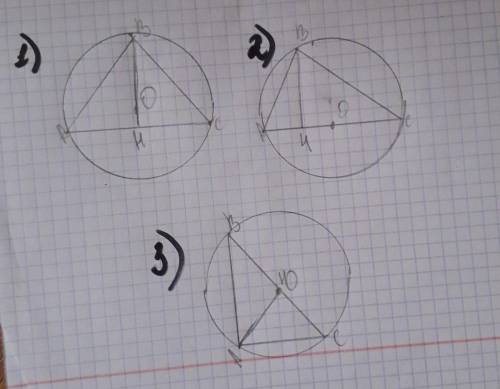
Первый треугольник:
AB=BC-гипотенуза
AB=BC-гипотенузаBH-высота(медиана)
AB=BC-гипотенузаBH-высота(медиана)BH-катет
AB=BC-гипотенузаBH-высота(медиана)BH-катетНС=АН-катет
AB=BC-гипотенузаBH-высота(медиана)BH-катетНС=АН-катетАС-диаметр
AB=BC-гипотенузаBH-высота(медиана)BH-катетНС=АН-катетАС-диаметрВС-хорда
Второй треугольник:
ВН-высота(медиана)
ВН-высота(медиана)АО-радиус
ВН-высота(медиана)АО-радиусАС-диаметр
ВН-высота(медиана)АО-радиусАС-диаметрВС-хорда
ВН-высота(медиана)АО-радиусАС-диаметрВС-хордаАВ и ВС-гипотенуза
ВН-высота(медиана)АО-радиусАС-диаметрВС-хордаАВ и ВС-гипотенузаВН-катет
АН и НС-катеты
Третий треугольеник:
АО-высота(медиана)
ВС-диаметр
АС-хорда
ВО-радиус
ВА и АС-катеты
ВС-гипотенуза
Иными словами, нам надо поместить квадрат в прямоугольный треугольник, вершинами которого являются точки (0;0); (-10;0) и (О;15)
Почему именно эти точки берем? Находим точки пересечения прямой с осями координат. Из уравнения прямой выразим у через х.
у/3=х/2+5, у=3х/2+15, если х=0, то у=15, Точка (0;15)-точка пересечения с осью оу, а если у=0, то х/2=-5, откуда х=-10, точка (-10;0)-точка пересечения прямой с осью ох.
Поскольку стороны у квадрата равны, то координата -х=у, и лежит на прямой, значит, удовлетворяет ее уравнению, вместо у подставим -х в уравнение и найдем точку, лежащую на прямой, и являющуюся вершиной R
х/2-(-х/3)=-5; х/2+х/3=-5, откуда 5/6х=-5, х=-6, у в этой точке равен 6. Значит, сторона квадрата равна 6, а его площадь 6²=36,
значит, площадь больше 30
ответ S(NOPR)>30
Центры их лежат на прямой, проходящей на равном расстоянии от заданных линий - это 4х+у-3=0.
Для того, чтобы получить уравнение конкретной окружности должны даваться данные для получения координат её центра.