по теореме Пифагора второй катет равен корень из 13^2-12^2т.е. = 5см;
расстояние от вершины прямого угла до гипотенузы и есть катет тот который мы нашли т.е. = 5см;
а площадь треугольника равна полупроизведение катетов т.е. (12*5)/2=30см
А₁А₂ = 2 см
Объяснение:
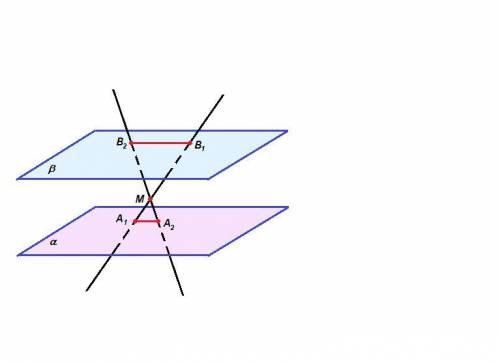
Если две параллельные плоскости пересечены третьей, то линии пересечения параллельны.
Пересекающиеся прямые А₁В₁ и А₂В₂ задают плоскость, которая пересекает плоскости α и β по прямым А₁А₂ и В₁В₂, значит
А₁А₂ ║ В₁В₂.
Тогда ∠МВ₁В₂ = ∠МА₁А₂ как накрест лежащие при пересечении параллельных прямых А₁А₂ и В₁В₂ секущей А₁В₁,
∠В₁МВ₂ = ∠А₁МА₂ как вертикальные, значит
ΔВ₁МВ₂ подобен ΔА₁МА₂ по двум углам.
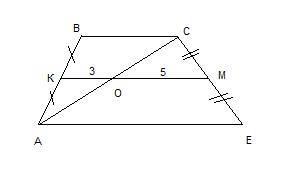
МВ₂ = А₂В₂ - МА₂ = 10 - 4 = 6 см
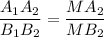
Пусть А₁А₂ = х, тогда В₁В₂ = х + 1,
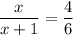
6x = 4(x + 1)
6x = 4x + 4
2x = 4
x = 2
А₁А₂ = 2 см
катет a=12, b-?,гипотенуза c=13
a) c^2=a^2+b^2; b^2=c^2-a^2; b=кв. корень из (c^2-a^2)
b=корень из (13^2-12^2)
b=корень из 169-144=кор из 25=5
б) S=1/2*a*b
S=1/2*12*13=78
в)Расстояние от вершины прямого угла до гипотенузы должно быть равно меньшему катету. В данном случае - 5.