ответ: 2688 см²
Объяснение:
В четырехугольник можно вписать окружность тогда и только тогда, когда суммы длин его противолежащих сторон равны.
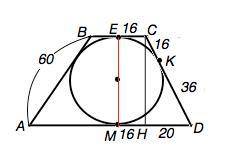
Для трапеции АВСD, в которую вписана окружность, BC+AD=AB+CD=60+16+36=112 см.
Стороны трапеции - касательные к вписанной окружности. Обозначим точки касания на ВС– Е, на СD - К, на AD-М. По свойству равенства отрезков касательных, проведенных из одной точки, СЕ=СК=16, DK=DM=36.
Соединим точки касания на основаниях отрезком ЕМ. Опустим высоту СН. МН=ЕС=16
DH=DM-CE=36-16=20.
По т.Пифагора СН=√(CD²-DH²)=√(52²-20²)=48 (см)
Площадь трапеции равна произведению полусуммы оснований на высоту.
S(ABCD)=0,5(BC+AD)•CH=0,5•112•48=2688 см².
Примем отрезки, на которые делится гипотенуза точкой касания, равными x и y.
Тогда один катет равен 1 + x, второй равен 1 + y (с учётом свойства касательных из одной точки к окружности).
Составим систему.
Первое уравнение: по Пифагору: (1 + x)² + (1 + y)² = 5²,
второе: x + y = 5.
Сделаем замену: у = 5 - х и подставим в первое уравнение.
(1 + x)² + (1 + (5 - х))² = 5².
1 + 2x + x² + 36 - 12x + x² = 25.
2x² - 10x + 12 = 0 или, сократив на 2:
x² - 5x + 6 = 0. Д = 25 - 4*1*6 = 1. х1 = (5 + 1)/2 = 3, х2 = (5 - 1)/2 = 2.
ответ: отрезки равны 3 и 2.