периметр паралелограмма - а+b+а+b=50 (где a.b - стороны параллелограмма)
т,к диагонали параллелограмма с и d деляться в точке пересечения пополам, следовательно можно записать разность периметров 2-х треугольниклов: (c/2+d/2+b) - (c/2+d/2+a)=5
раскрываем скобки: c/2+d/2+b-c/2-d/2-a=5
упрощаем : b-a=5
получили систему: a+b+a+b=50
2a+2b=50
упрощаем и получаем систему: a+b=25 (1)
b-a=5 (2)
решаем, выразим во (2) уравнении b через a , т.е b=5+a и в (1) подставим вместо b: a+ 5+a=25
решаем 2a=25-5.
a=10
теперь полученный результат т,е а=10, подставим во (2) уравнение и найдем b:
b-10=5.
b=5+10.
b=15
ответ:a=10. b=15
периметр паралелограмма - а+b+а+b=50 (где a.b - стороны параллелограмма)
т,к диагонали параллелограмма с и d деляться в точке пересечения пополам, следовательно можно записать разность периметров 2-х треугольниклов: (c/2+d/2+b) - (c/2+d/2+a)=5
раскрываем скобки: c/2+d/2+b-c/2-d/2-a=5
упрощаем : b-a=5
получили систему: a+b+a+b=50
2a+2b=50
упрощаем и получаем систему: a+b=25 (1)
b-a=5 (2)
решаем, выразим во (2) уравнении b через a , т.е b=5+a и в (1) подставим вместо b: a+ 5+a=25
решаем 2a=25-5.
a=10
теперь полученный результат т,е а=10, подставим во (2) уравнение и найдем b:
b-10=5.
b=5+10.
b=15
ответ:a=10. b=15
а) BC1 || AD1, поэтому угол между прямыми AB1 и BC1 равен углу между AB1 и AD1.
ребро куба равно а, поэтому (так как грани куба - квадраты), то AB1=AD1=B1D1, а значит треугольник AB1D1 - правильный(равносторонний),
углы равностороннего треугольника равны 60 градусов,
значит искомый угол между прямыми AB1 и BC1 равен 60 градусов
б) так как В1С1 - перпендикуляр с точки С1 на грань АА1В1В, то угол между прямой AC1 и гранью AA1B1B равен углу В1АС1
(треугольник АВ1С1 - прямоугольным с прямым углом АВ1С1)
по свойству диагонали квадрата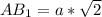
по свойству диагонали куба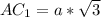
угол В1АС1 равен arccos корень(2/3)т.е.
угол между прямой AC1 и гранью AA1B1B равен arccos корень(2/3) градусов