Отрезки МК и NP параллельны соседним сторонам прямоугольника, => соответственно равны им, пересекаются под прямым углом и делят АВСD на 4 прямоугольника, (неважно, равной или разной площади). Обозначим точку пересечения МК и NP буквой О.
а)
Стороны четырехугольника МNKP являются диагоналями получившихся прямоугольников и делят каждый из них пополам (свойство). Поэтому площадь MNKP равна сумме площадей этих половин, т.е. равна половине площади ABCD.
б)
Площадь выпуклого четырехугольника равна половине произведения его диагоналей на синус угла между ними.
Так как S(ABCD)=AB•CD, МК=АD и NP=AB, а sin90°=1, то S(MNKP)=MK•NP•sin90°=0,5•S(ABCD).
в)
S(MNKP)=S∆MNP+S∆NKP=0.5•MO•NP+0.5•KO•NP=0,5•NP•(MO+OK) => S(MNKP)=0,5•NP•MK =>
S(MNKP) =0,5•S(ABCD), т.к. NP=AB и МК=АD

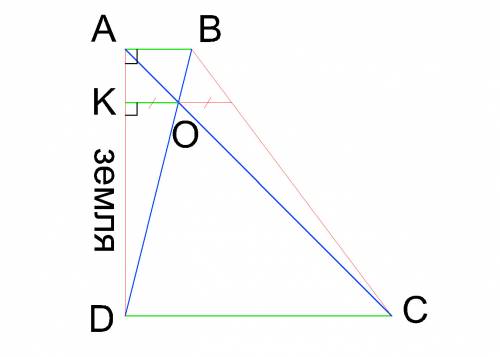
Шесты АВ и ДС как основания образуют прямоугольную трапецию АВСД, а пересечение канатов ВД и СА есть не что иное, как пересечение диагоналей прямоугольной трапеции.
Как известно, отрезок, параллельный основаниям и проходящий через пересечение диагоналей прямоугольной трапеции делится точкой пересечения пополам, и если АВ=х, ДС=у, то длина его равна 2·х·у/(х + у).
Исходя из этого: ОК=2·х·у/(х + у)÷2=х·у/(х + у)
1) ОК=(х·у)÷(х + у)
Как видно, длина ОК никаким образом не зависит от расстояний между шестами, а лишь от их высоты.
2) Если AB=х=2 м, а DC=у=8 м, то ОК=(2·8)÷(2+8)=1,6 м
ответ: длина шеста ОК=1,6 м
sбок=2πrh => 12π=2πr3
=> r=2
sполн=2πr(h+r)=2π(3+2)=10π
если хочешь более точнее:
π=3.14 тогда sполн=10·3.14=31.4