Если взять куб ABCDA1B1C1D1, то фигура с вершинами A1BC1D - правильный тетраэдр. Поэтому проекция точки С1 на плоскость A1BD - это центр правильного треугольника A1BD - пусть это точка Q1.
У пирамиды AA1BD основание A1BD - правильный треугольник, и все боковые ребра равны (это ребра куба). Поэтому проекция точки A на плоскость A1BD - это центр правильного треугольника A1BD - точка Q1. Поскольку есть только одна прямая, перпендикулярная плоскости A1BD и проходящая через заданную точку Q1 - центр треугольника A1BD, то AC1 перпендикулярно A1BD.
что и требовалось доказать.
Если провести еще одну плоскость - B1D1C, то она тоже перпендикулярна AC1 (доказывается точно так же, пусть центр треугольника B1D1C - точка Q2), то есть параллельна плоскости BDA1.
Поэтому эти две плоскости (поскольку они параллельны) отсекают на разных прямых пропорциональные отрезки. То есть AQ1/Q1Q2 = AM/MC (М - центр грани ABCD) и Q1Q2/Q2C1 = A1M1/M1C1 (М1 - центр грани A1B1C1D1).
Поэтому плоскости A1BD и B1D1C делят AC1 на три равных отрезка.
что и требовалось доказать.
Расстоянием от центра до плоскости будет ОL. ОL перпендикулярна плоскости ABS. Так как OL перпендикулярна SM по постороению.Также OL перпендикулярна АВ. AB перпендикулярна всей плоскости SOM по теореме о 3-х перпендикулярах. Значит и  Если прямая перпендикулярна двум непараллельным прямым в плоскости, то она перпендикулярна всей плоскости.
Если прямая перпендикулярна двум непараллельным прямым в плоскости, то она перпендикулярна всей плоскости.
Рассмотрим треугольник SOM. Он - прямоугольный. Теперь найдем неизвестный катет ОМ. Его можно узнать из прямоугольного треугольника в основании конуса 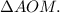 Так как АМ=МВ=3, так как SM - является высотой, биссектрисой и медианой в равнобедренном треугольнике ASB (AS=BS).
Так как АМ=МВ=3, так как SM - является высотой, биссектрисой и медианой в равнобедренном треугольнике ASB (AS=BS).
У треугольника АОМ гипотенуза ОА=5 см, АМ=3см. Надо узнать только ОМ. По теореме Пифагора
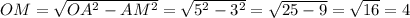
Теперь снова обратим внимание на треугольник SOM. Два катета у него уже известны. SO=12 см как высота конуса. Теперь найдем гипотенузу SM по той же теореме Пифагора.
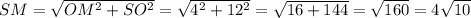
Найдем синус угла М в треугольнике SOM.
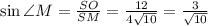
Теперь из прямоугольного треугольника MOL найдем катет OL, зная гипотенузу ОМ.
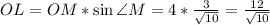
ответ: расстояние от точки О до плоскости сечения равно 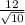
180-140=40
ответ:угол при основании равен 40 градусов