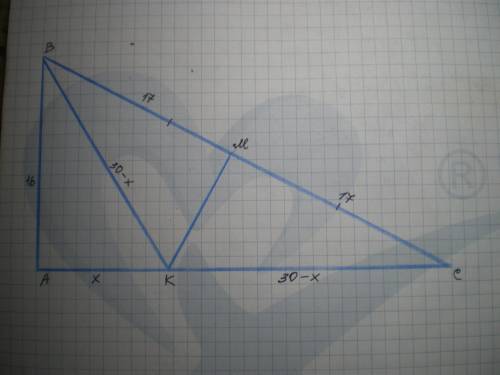
Дано: ΔАВС - прямокутний, ∠А=90°, АС=30 см, ВС=34 см; МК⊥ВС, ВМ=МС. Знайти МК.
Знайдемо АВ за теоремою Піфагора:
АВ=√(ВС²-АС²)=√(1156-900)=√256=16 см.
Проведемо ВК і розглянемо ΔВКС - рівнобедрений, тому що ВМ=СМ і МК⊥ВС, отже ВК=КС.
Нехай АК=х см, тоді КС=ВК=30-х см.
Знайдемо АК з ΔАВК - прямокутного:
АВ²=ВК²-АК²; 16² = (30-х)² - х²; 256=900-60х+х²-х²;
60х=900-256=644; х=10 11/15 см. АК=10 11/15 см, тоді
ВК = 30 - 10 11/15 = 19 4/15 = 289/15 см.
Знайдемо МК за теоремою Піфагора з ΔВМК, де ВМ=34:2=17 см.
МК²=ВК²-ВМ²=(289/15)² - 17² = (83521/225) - 289 = 18496/225.
МК=√(18496/225)=136/15=9 1\15 см.
Відповідь: 9 1/15 см.
2.
Так как в равнобедренном треугольнике боковые стороны равны, а биссектриса делит сторону пополам, то АВ = ВС, АВ/2 = ВС/2, ДА= АВ/2 и ЕС= ВС/2 и следовательно ДА=ЕС.
В треугольнике АДС и СЕА
ДА=ЕС
АС - общая
угол С = углу А т.к треугольник АВС равнобедренный
Следовательно треугольники равны по двум сторонам и углу между ними.
1.
Рассмотрим треугольники АКД и КДС: АД=ДС, КД - общая, угол Д прямой, т.к. ВД - медиана. отсюда следует что треугольники АКД = КДС, следовательно и все стороны равны, в том числе и стороны АК = КС (треугольник равнобедренный)