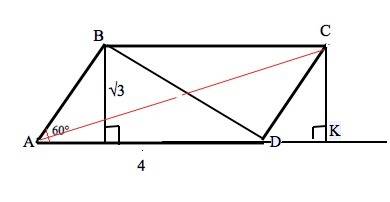
Рассмотрим ∆ АВН.
Угол ВАD=60°, АВ=АН/sin 60°=√3:(√3/2)=2 ⇒ АН=АВ•cos60°=2•0,5=1
Из прямоугольного ∆ ВНD по т.Пифагора ВD²=BH²+DH²=3+9=12
Найдем АС.
Сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон.
ВD²+АС²=2•( AB²+AD²)
12+AC²+2•(4+16) ⇒ AC² =28 откуда AC=2√7 см
Опустим высоту СК на продолжение стороны АD.
∆ ABH=∆ CDK ( равные соответственные углы при А и D и равные катеты ВН=СК).⇒
AK=AD+DK=5⇒
АС=√(CK²+AD²)=√28=2√7 см
теорема косинусов, (угол АВD=180°-60°=120°). Вычисления приводить не буду, они дадут тот же результат.
Три медианы треугольника делят его на 6 равновеликих частей, т.к. каждая по отдельности делит на 2 равных по площади части.
Тогда S ∆ АОВ=2•¹/₆ S ∆ ABC=¹/₃ S ∆ ABC
Площадь треугольника равна половине произведения его сторон на синус угла между ними.
S AOB=AO•BO•sin ∠AOB:2
sin120º=(√3):2
Медианы треугольника точкой их пересечения делятся в отношении 2:1, считая от вершины.
Тогда АО=12:3•2=8,
BO=15:3•2=10
S AOB=[8•10•(√3):2]:2=20√3 (ед. площади)
S ∆ ABC=3 S∆ AOB=60√3 (ед. площади)