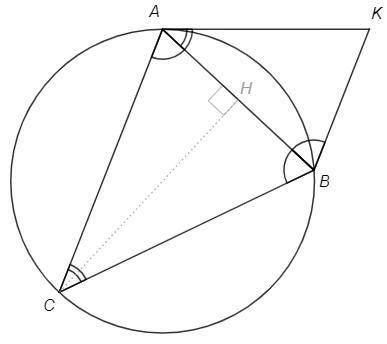
a) Вписанный угол равен половине дуги, на которую опирается.
ACB=∪AB/2
Угол между касательной и хордой равен половине дуги, стягиваемой хордой.
KAB=∪AB/2
Следовательно ACB=KAB
б) CAB=KBA (накрест лежащие при AC||KB)
△ACB~△BAK (по двум углам)
△ACB - равнобедренный => △BAK - равнобедренный
(AC/BA=BC/KA, AC=BC => BA=KA)
в) Отношение площадей подобных фигур равно коэффициенту подобия (то есть отношению соответствующих сторон).
S(ACB)/S(BAK)= (AC/AB)^2
Стороны треугольника пропорциональны синусам противолежащих углов - если известны углы, то известно и отношение сторон. В равнобедренном треугольнике достаточно знать один угол (и его расположение), чтобы найти остальные углы. Таким образом в равнобедренном треугольнике ACB достаточно знать угол C, чтобы найти отношение сторон AB и AC.
(Высота CH является медианой и биссектрисой.
CHA=90, AH=AB/2, ACH=C/2
AH/AC =sin ACH => AB/AC =2sin C/2)
Сторона основания - а, определится через диагональ основания = 8*cos60*2=8*0,5*2=8. a = 8/√2
1) Площадь боковой поверхности S = 4s = 4(а * апофему)/2
апофема =√ [(a/2)²+h²]=√[(4/√2)²+(4√3)²=√(8+16/3). S = 2*(8/√2)*√(8+16/3)
2) Объем V = Sоснования*h/3 = a²h/3 = (8/√2)²4√3/3 = 128/3√3
3) Для определения угла между гранями выполним вертикальное сечение пирамиды.
В сечении получим равнобедренный треугольник со стороной равной апофеме и основанием а. α = 2 arcsin (8/2√2)/√(8+16/3)