1)в прямоугольном треугольнике катеты равна 8 см и 15 см.найти периметр треугольника. 2)из одной точки к данной прямой проведены две равные наклонные.найти расстояние между основаниями наклонных,если проекция одной из них равна 16 см. 3)доказать,что сумма диагоналей трапеции больше суммы её оснований.

👇

Увидеть ответ

Ответ:

albina0101011

21.03.2023

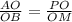
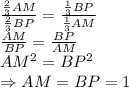
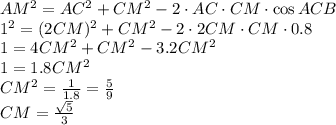
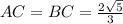
1) По теореме Пифагора:

АВ² = АС² + ВС²

АВ² = 8² + 15² = 64 + 225 = 289

АВ = √289 = 17 см

2) Прямая а и наклонные АВ и АС.

АВ = АС по условию.

В и С - основания наклонных, значит найти надо отрезок ВС.

Пусть АН⊥а, тогда ВН = 16 см - проекция наклонной АВ на прямую а.

ΔАВС равнобедренный, АН - высота и медиана (по свойству равнобедренного треугольника), ⇒

ВС = 2ВН = 2 · 16 = 32 см

3) Доказать: AD + BC < AC + BD

В треугольнике каждая сторона меньше суммы двух других его сторон.

ΔAOD: AD < AO + OD

ΔBOC: BC < BO + OC

Складываем эти неравенства:

AD + BC < AO + OD + BO + OC, ⇒

AD + BC < AC + BD

1)в прямоугольном треугольнике катеты равна 8 см и 15 см.найти периметр треугольника. 2)из одной точ

4,7(88 оценок)

Открыть все ответы

Ответ:

Макси00084322233

21.03.2023

Пусть О - точка пересечения медиан треугольника АВС. Треугольники AOP и BOM подобны по двум углам (два угла равны по условию, еще два угла вертикальные). Тогда:
$\frac{AO}{OB} = \frac{PO}{OM}$
Так как медианы точкой пересечения делятся в отношении 2:1, то:
$\frac{ \frac{2}{3} AM}{ \frac{2}{3} BP} = \frac{\frac{1}{3}BP}{\frac{1}{3}AM}
\\\
\frac{ AM}{ BP} = \frac{BP}{AM}
\\\
AM^2=BP^2
\\\
\Rightarrow AM=BP=1$
Если медианы, проведенные к двум сторонам треугольника равны, то и сами стороны также равны. Значит, АС=ВС и треугольник АВС равнобедренный.
Рассмотрим треугольник АМС. По теореме косинусов, учитывая соотношение АС=2СМ, получим:
$AM^2=AC^2+CM^2-2\cdot AC\cdot CM\cdot\cos ACB
\\\
1^2=(2CM)^2+CM^2-2\cdot 2CM\cdot CM\cdot0.8
\\\
1=4CM^2+CM^2-3.2CM^2
\\\
1=1.8CM^2
\\\
CM^2= \frac{1}{1.8} = \frac{5}{9} 
\\\
CM= \frac{ \sqrt{5} }{3}$
Следовательно стороны в два раза больше: $AC=BC= \frac{2 \sqrt{5} }{3}$
Тогда площадь треугольника найдем как половину произведения двух его сторон на синус угла между ними:
$S= \frac{1}{2} \cdot AC\cdot BC\cdot \sinACB
\\\
S= \frac{1}{2} \cdot AC^2\cdot \sqrt{1-\cos ACB} 
\\\
S= \frac{1}{2} \cdot ( \frac{2 \sqrt{5} }{3})^2\cdot \sqrt{1-0.8}=\frac{1}{2} \cdot \frac{4\cdot5 }{9} \cdot \frac{3}{5} = \frac{2}{3}$
ответ: 2/3

4,4(4 оценок)

Ответ:

vlad22803

21.03.2023

Обычно в задачах на параллельные прямые есть две прямые и секущая. Отсюда мы узнаем три новых правила.
1.Накрест лежащие углы при секущей равны. ( Если Один угол находится снизу,допустим справа, а другой слева вверху и наоборот)
2. Соответственное углы при секущей равны.( Один угол находится над нижней прямой, а другой на верхней прямой)
3. Сумма односторонних углов при секущей равна 180 градусов. ( Находятся на одной стороне)
Все углы обычно обозначаются так: угол 1,2,3,4,5,6,7,8.
Также тебе пригодятся знания о вертикальных углах
Можете объяснить понятно как решаются по на тему параллельные прямые. например напишите какую-нибудь