Объяснение:
Из условия нам известно, что ∠DOC равен пяти углам COB.
Если посмотреть на чертеж, то мы увидим, что ∠DOC и ∠COB смежные, а следовательно, их сумма равна 180°. Для нахождения углов DOC и COB составим линейное уравнение:
Пусть x - ∠DOC, тогда ∠COB - 5x. (угол COB равен 5x, т.к. он в 5 раз больше угла DOC)
Получаем:
x + 5x = 180°
6x = 180°
x = 30° (Это мы нашли x, то есть ∠DOC)
∠COB = 30° * 5 = 150°.
Ну а дальше - дело техники.
∠COD = ∠BOA = 150°(все вертикальные углы равны)
∠BOC = ∠AOD = 30°(все вертикальные углы равны).
Задача решена.
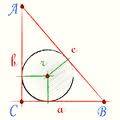
r = (a+b-c)/2 , где а,b - катеты, с - гипотенуза, тогда
4 = (а+b -26)/2
а+b -26 = 8
а+b = 34
Таким образом Р = а+b +с =34+26 =60 (см).
2) Правило:
отрезки касательных к окружности, проведённые из одной точки, равны, т.е.
ВМ =ВР=5, АМ=АТ=12, СТ=СР = х, тогда по теореме Пифагора:
(5 + х)²+(12 + х)²=17²
25 + 10х + х² +144 +24х +х² = 289
2·х² +34х+169 - 289 =0
2·х² +34х -120 =0
х² + 17х -60 =0
х₁ = 3; х₂= -20 ( не подходит по смыслу задачи)
Таким образом АС = 15, ВС = 8 и Р= 15+8+17 = 40 (см).
360\5=72 т.к окружность=360 градусов.