Чертёж смотрите во вложении.
Дано:Четырёхугольник ABCD — равнобедренная трапеция (AD и ВС — боковые стороны, АВ и DC — основания).
DB и АС — диагонали.
Е — точка пересечения диагоналей.
∠DEC = 90°.
FG — высота.
НI — средняя линия = 6 см.
Найти:S(ABCD) = ?
Решение:Если у равнобедренной трапеции диагонали взаимно перпендикулярны, то высота равна средней линии.
То есть -
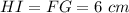
Площадь трапеции равна произведению средней линии и высоты.
То есть -
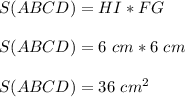
(А вообще, можно сформулировать такую теорему — Если у равнобедренной трапеции диагонали взаимно перпендикулярны, то площадь этой трапеции равна квадрату её высоты (или средней линии.)
ответ: 36 см².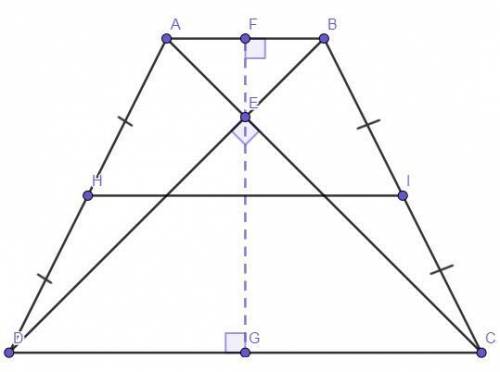
диагональ меньшего основания: 2√2
диагональ большего основания: 10√2
Н² = 26² - (4√2)² = 644
Н = 2√161
2) рисунок похожий)))
сначала нужно найти сторону меньшего основания...
часть основания: х² = 26² - 24² = 2*50
х = 10
сторона меньшего основания: 25-10*2 = 5
и дальше решение по той же схеме...
диагональ меньшего основания: 5√2
диагональ большего основания: 25√2
Н² = 26² - (10√2)² = 476
Н = 2√119