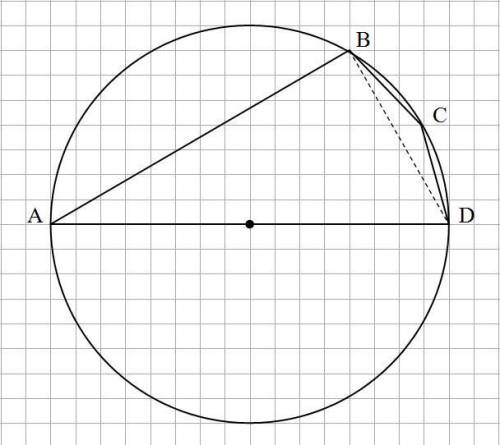
См. рис.
Так как AD - диаметр окружности, то угол ∠ABD = 90°
Следовательно, оставшийся угол прямоугольного
треугольника ΔABD: ∠BAD = 90 - 65 = 25°
Так как угол ∠BAD - вписанный, то величина дуги, на которую он опирается:
∪BCD = 2 · ∠BAD = 50°
Искомый угол ∠С = ∠BCD опирается на оставшуюся дугу
окружности:
∪BAD = 360 - ∪BCD = 360 - 50 = 310°
И величина угла ∠С = 310 : 2 = 155°
Причем, величина угла ∠С не зависит от местоположения точки С на дуге ∪BCD, так как в любом случае этот угол опирается на дугу ∪BAD, равную 310°
а)
Сейчас поэкспериментируем!
Формула вычисления суммы углов многоугольника такова: 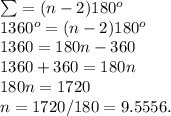
Как мы видим — число не целое, что и означает, что правильный многоугольник, чъя сумма углов равна 1360° — не сущестувет.
б)
Фромула вычисления внуреннего угла в правильном многоуольнике такова:
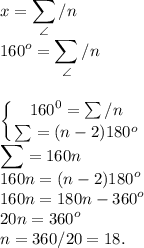
Количество углов — 18, сумма углов: (18-2)180 = 2880°, каждый внутренний угол равен: 160°.
Да, такой многоугольник может существовать.
в)
Нет, наоборот: радиус описанной окружности больше радиуса вписанной окружности.
Например есть теорема, что радиус описанной окружности около правильного треугольника — в 2 раза больше радиуса вписанной окружности в этот же треугольник.
Один из концов радиуса описанной окружности — не лежит на нём, и не находится в мноугольнике, в то время как радиус вписанной окружности — можно провести через вершины многоугольника до центра окружности.
ответ: 3√5 см
Объяснение: