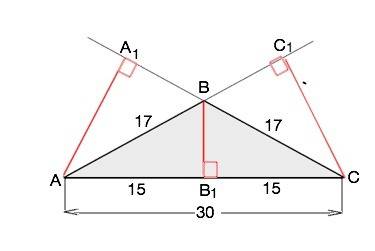
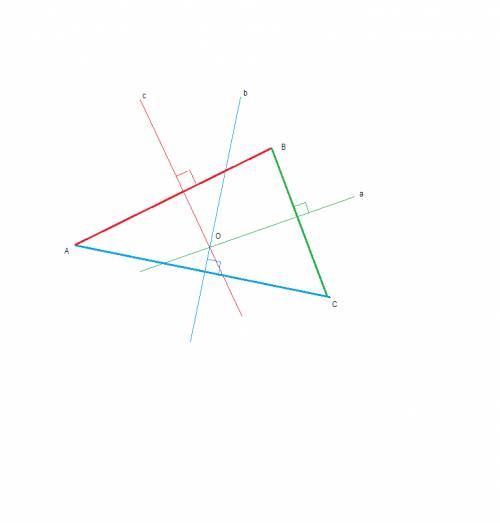Назовём данный треугольник АВС.
ВВ1- высота к АС.
АА1=СС1 - высоты к равным боковым сторонам.
Высота равнобедренного треугольника, проведенная к основанию, является его биссектрисой и медианой. ⇒
АВ1=СВ1=30:2=15 см
∆ АВВ1=∆ СВВ1 ( по трем сторонам).
Из ∆ АВВ1 по т.Пифагора
ВВ1=√(AB²-AB1²)=√(17²-15²)=8 см
Высоты к боковым сторонам найдем из площади ∆ АВС
Заметим, что ∆ АВС - тупоугольный ( АС² > АВ²+ВС²), поэтому высоты, проведенные к боковым сторонам тупоугольного треугольника, лежат вне его.
S(ABC)=BB1•AC:2=8•15=120 см²
AA1=2S(ABC):BC
AA1=CC1=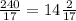 см
см
1)
треугольник АВС
к каждой стороне проводим серединный перпендикуляр
к стороне АВ - серединн. перпендикуляр -с
к стороне ВС - серединн. перпендикуляр -а
к стороне АС - серединн. перпендикуляр -b
точка пересечения перпендикуляров О - равноудалена от всех вершин
2)
угол АВС
DE - прямая пересекает стороны угла
строим биссектриссы
BB1 - биссектриса <B
DD1 -биссектриса <BDE
EE1 - биссектриса <DEB
точка пересечения биссектрис О равноудалена от от прямой,пересекающей стороны угла и от сторон данного угла
3)
также как и пункте 2) через биссектрисы
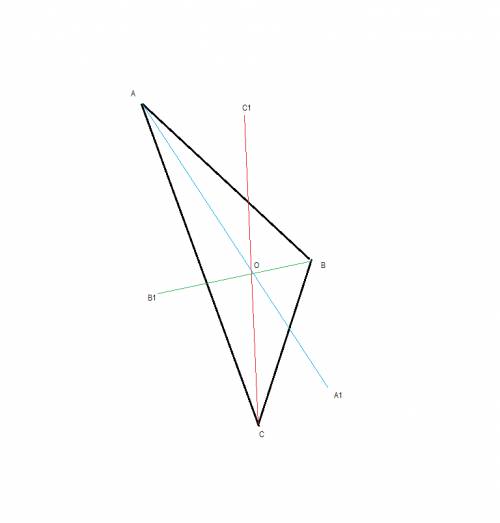
треугольник АВС
строим биссектриссы
BB1 - биссектриса <B
AA1 -биссектриса <A
CC1 - биссектриса <C
точка пересечения биссектрис О равноудалена от трех сторон треугольника