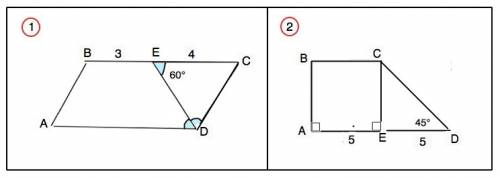
1) В параллелограмме противолежащие стороны равны и параллельны, противолежащие углы равны.
ДЕ - биссектриса, ⇒∠ЕDА=∠ЕDС.
∠СЕD=∠ЕDА – накрестлежащие. ⇒
треугольник СЕD равнобедренный, а так как углы при основании ЕD равны 60°, он - равносторонний.
Угол С=60°, угол А=угол С=60°. Сумма углов параллелограмма, прилежащих к одной стороне, равна 180°. ⇒∠В=∠D=120°
СD=ЕС=АС=4 см. АD=ВС=3+4=7 см
Р (АВСD)=2•(7+4)=22 см
Четырехугольник АВЕD - равнобедренная трапеция, так как ВЕ║|АD, и АВ=СД⇒АВ=ЕД.
-------------------
2) ∆ СЕD прямоугольный, Сумма острых углов прямоугольного треугольника 90°. ⇒
угол ЕСD=90°- 45*=45°⇒ ∆ СЕD – равнобедренный.
CE=ED=5
Перпендикуляр СЕ параллелен и равен АВ. -⇒
АВ=СЕ=5 см
8см,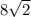 
см
Объяснение:
Наш треугольник прямоугольный и один из углов 45°, значит третий угол треугольника равен 90° - 45° = 45°.
Получается, что в треугольнике 2 равных угла по 45°, следовательно данный треугольник равнобедренный, следовательно катеты 
и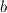 
равны, то есть второй катет тоже 8 см.
Гипотенузу 
находим по теореме Пифагора:
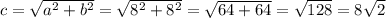(см)
P.S
Признак равнобедренного треугольника: если два угла треугольника равны, то такой треугольник равнобедренный
Теорема Пифагора: квадрат гипотенузы равен сумме квадратов катетов
R=5√3/(2*√2/2)=5√3/√2=5√6/2
S=πR²=25*6π/4=150π/4=37,5π
C=2πR=2π*5√6/2=5π√6
r=a/2tg45
r=5√3/2
S=π*75/4=18,75π
C=2π*5√3/2=5π√3