
1.1800 градусов
2.Площадь параллелограмма равна произведению его основания (a) на высоту (h):
S = a ⋅ h
144 см² = а ⋅ 16 см
a = 9 см
3.Из условия известно, что гипотенуза равна 13, а один из катетов 12. Для того, чтобы найти площадь прямоугольного треугольника будем использовать следующую формулу:
S = 1/2 * a * b, где a и b — катеты прямоугольного треугольника.
Давайте по теореме Пифагора найдем длину второго катета.
Квадрат гипотенузы равен сумме квадратов катетов.
a2 + b2 = c2;
122 + x2 = 132;
144 + x2 = 169;
x2 = 169 - 144;
x2 = 25;
x = 5.
Ищем площадь прямоугольного треугольника:
S = 1/2 * 12 * 5 = 30 кв. единиц.
ответ: 30 кв. единиц.
4.Площадь ромба можно найти по формуле S = 0,5d₁d₂, где d₁ и d₂ - его диагонали.Т.к. ромб - это параллелограмм, у которого все стороны равны, то он обладает всеми свойствами параллелограмма, а именно: диагонали ромба точкой пересечения делятся пополам. Значит, полусумма диагоналей равна 28 : 2 = 14 (см).Свойство ромба: диагонали ромба перпендикулярны. Значит, при пересечении диагоналей ромба получаются 4 прямоугольных треугольника, у которых катеты - половины диагоналей, а гипотенуза - сторона ромба.Рассмотрим один из прямоугольных треугольников и, применив теорему Пифагора, найдем его катеты.
Пусть один из катетов х см, тогда второй будет равен (14 - х) см. Т.к. сторона ромба равна 10 см, то составим и решим уравнение:
х² + (14 - х)² = 10²,
х² + 196 - 28х + х² - 100 = 0,
2х² - 28х + 96 = 0,
х² - 14х + 48 = 0.
D = (-14)² - 4 · 1 · 48 = 196 - 192 = 4; √4 = 2
х₁ = (14 + 2)/(2 · 1) = 16/2 = 8, х₂ = (14 - 2)/(2 · 1) = 12/2 = 6
Если один из катетов равен 8 см, то второй будет равен 14 - 8 = 6 (см). Тогда диагонали ромба будут равны 16 см и 12 см, а площадь
S = 0,5 · 16 · 12 = 96 (см²)
Если один из катетов равен 6 см, то второй будет равен 14 - 6 = 8 (см). Тогда диагонали ромба будут равны 12 см и 16 см, а площадь
S = 0,5 · 12 · 16 = 96 (см²)
ответ: 96 см².
Объяснение:
Задача
Дано:
периметр равностороннего треугольника 18 см
периметр равнобедренного треугольника 20 см
Сторона равностороннего треугольника является основанием равнобедренного треугольника
Найти: стороны равнобедренного треугольника
Решение
1) 18:3=6 (см) - сторона равностороннего треугольника;
2) пусть боковые стороны равнобедренного треугольника равны х см, тогда
х +х + 6 = 20
2х=20-6
2х=14
х=7 (см) - боковые стороны равнобедренного треугольника;
ответ: стороны равнобедренного треугольника равны 6 см, 7 см и 7 см.
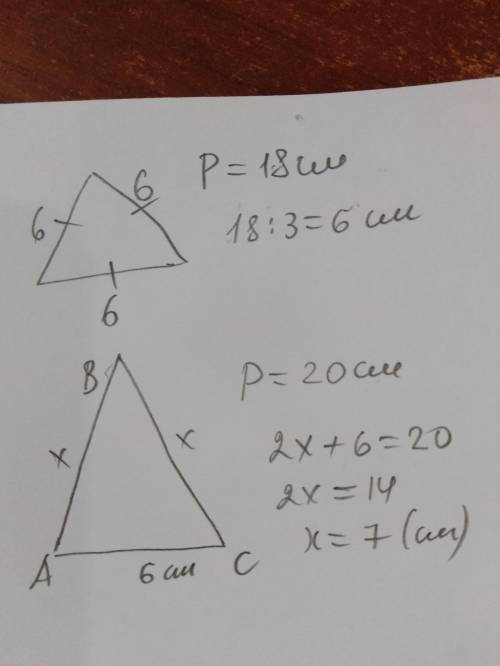
CH_|_AB
(ABD)∧(ABC)=<DHC
AB=√CB²+CA²=√49+576=√625=25
AH=x,BH=25-x
CH²=CA²-AH²=CB²-BH²
49-x²=576-625+50x-x²
50x=98
x=1,96
CH²=49-3,8416=45,1584
CH≈6,72
tg<DHC=DC/CH≈1,4881
<DHC=56гр 6мин