Высоат БД поделила треугольник АБС на два прямоугольных треугольника,Рассмотрим один из них - АДБ.В нём катет БД лежит против угла в 30 ,отсюда следует ,что катет равен одной второй гипотенузы АБ,равен 12 см.
Далее находим оставшийся угол треугольника АБС .Угол С = 180 - (75+30)=75,отсюда следует,что АС=АБ=12.Площадь ищем по формуле: одна вторая произведения основания на высоту.АС * БД : 2 = 12 *6 :2 =36 см квадратных
85+5√119см²
Объяснение:
Дано:
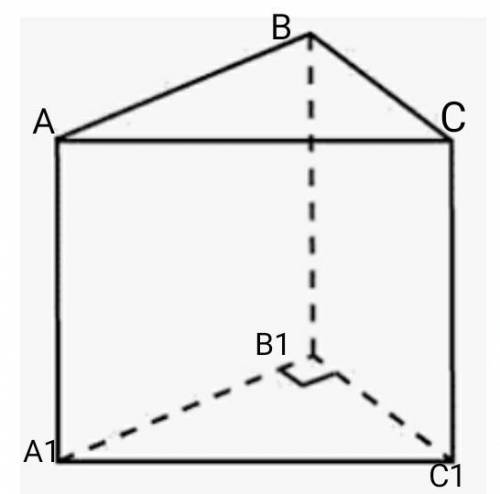
ABCA1B1C1- прямая призма.
∆А1В1С1- прямоугольный.
А1В1=5см
А1С1=12см.
Sбок=?
Решение.
По теореме Пифагора найдем второй катет ∆А1В1С1
С1В1²=А1С1²-А1В1²=12²-5²=144-25=119 см
С1В1=√119 см
√25>√119
5>√119 значит
АВА1В1- является квадрат.
А1В1=В1В=АВ=АА1=5см.
ВВ1=5см высота призмы.
Формула нахождения площади боковой поверхности призмы.
Sбок=Росн*h, где Росн- периметр основания, h=BB1 - высота.
Росн=А1В1+В1С1+А1С1=12+5+√119=
=17+√119 см периметр треугольника.
Sбок=(17+√119)*5=85+5√119 см² площадь боковой поверхности призмы.
Объяснение:
№3
<1+<2=180°
Пусть градусная мера угла <1 будет 2х°, тогда градусная мера угла <2 будет 7х°.
Составляем уравнение.
2х+7х=180°
9х=180
х=180/9
х=20
2*20=40° градусная мера <1;
7*20=140° градусная мера угла <2.
<3=<2, вертикальные углы.
<3=140°
ответ: <3=140°
№4
<2+<1=180°
Пусть градусная мера угла<1 будет х°, тогда градусная мера угла <2 будет 4х°.
Составляем уравнение
х+4х=180
5х=180
х=180/5
х=36° градусная мера угла <1;
4*36=144° градусная мера угла <2
<1=<3, вертикальные углы
<3=36°
ответ: <3=36°
Для начала мы должны найти третий угол треугольника:
180-30-75=75.
Треугольник равнобедренный (что можно понzть из условия), а боковые стороны его равны 12см.
Угол между этими сторонами = 30градусов
По формуле площади треугольника
S=1/2*a*a*sin a, где a -альфа
S = (1/2)*12*12*sin30 =3*12 = 36см^2