√2
Объяснение:
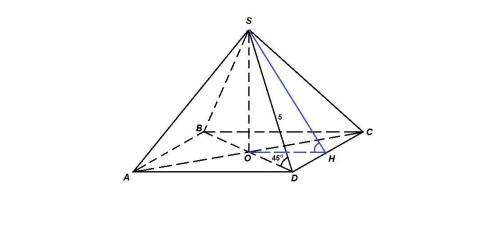
Пирамида правильная, значит в основании лежит квадрат, а боковые грани равные равнобедренные треугольники.
SO - высота пирамиды, значит DO - проекция бокового ребра SD на плоскость основания, тогда
∠SDO = 45° - угол наклона бокового ребра к плоскости основания.
Пусть Н - середина CD. тогда
SH⊥CD, так как медиана равнобедренного треугольника CSD является и высотой и
ОН⊥CD (ОН - средняя линия ΔACD, значит ОН║AD, а AD⊥CD), тогда
∠SHO - угол наклона боковой грани к плоскости основания - искомый.
______
ΔSOD: ∠SOD = 90°, ∠SDO = 45°, значит ∠OSD = 45°, треугольник равнобедренный,
SO = OD = SD / √2 = 5/√2 см
Диагонали квадрата равны, перпендикулярны и точкой пересечения делятся пополам, значит
OC = OD, ΔCOD равнобедренный, прямоугольный, CD - его гипотенуза:
CD = OD√2 = 5/√2 · √2 = 5 см
ОН = CD/2 = 2,5 см как медиана прямоугольного треугольника, проведенная к гипотенузе.
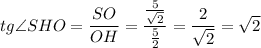
Гегель использует термин Mittelasien для обозначения области, населённой монголами. Термин «Средняя Азия» зафиксирован в трудах историка С. М. Соловьёва, под которым понимается степной географический регион к юго-востоку от Русской равнины и востоку от Каспийского моря.
В древности в Средней Азии существовали довольно крупные государства. В VII—V вв. до н. э. в долине Зарафшана существовало государство Согдиана, в среднем течении Амударьи — Бактрия, в нижнем её течении — Хорезм, в долине Мургаба — Маргиана. Северная часть Средней Азии входила в состав Скифии, а южная часть находилась в сфере влияния Ирана.
Первые сведения о Средней Азии встречаются в трудах Геродота, Страбона, Арриана, Птолемея и других.
Ну тут уже понятно что центр окружности-это точка, равноудалённая от всех точек, принадлежащих окружности.
Радиус-это отрезок от центра до любой точки окружности.