1. Решение: пусть в равнобедренном треугольнике АВС АС - основание, АВ и ВС - боковые стороны, равные по 13 см, ВМ медиана, равная 5см.
Так как треугольник равнобедренный, ВМ - высота данного треугольника, АМ = МС и треугольники АВМ и СВМ равны.
АМ = 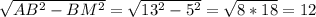 см
см
АС = 2*АМ = 24см
Р = 13 + 13 + 24 = 50см
S = 1/2 * ВМ * АС = 1/2 * 5 * 24 = 60см
2. во 2 задаче вы не написали чему равен угол D, пусть он будет α.
S = 1/2 * h (BC + AD)
h = CD * sinα
S = 1/2 * 10 * sinα (13 + 27) = 5*40 * sinα
Подставите значение угла D и получите ответ
3. Если в окружности пересекаются 2 хорды, то произведения их отрезков равны.
AM*MB = DM*MC = 120см
Составляем систему:
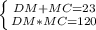
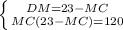
Работаем со вторым уравнением МС(23-МС) = 120
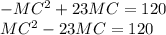
Решаем через дискриминант
D = 529 - 4*120 = 49
МС₁ = (23-7)/2 = 8
МС₂ = (23 + 7)/2 = 15
Подставляем в первое уравнение:
DM₁ = 23 - 8 = 15
DM₂ = 23-15 = 8
Значит, СМ и DM равны 8 и 15 см, или 15 и 8 см соответственно
4. Прямоугольный треугольник АВС (прямой угол С) вписан в окружность, значит центр окружности делит его гипотенузу на 2 одинаковые части. Гипотенуза данного треугольника АВ будет равна диаметру окружности, то есть 13 см.
катет ВС = 5см
АС = 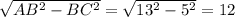 см
см
S = 1/2 * АС * ВС = 1/2 * 5 * 12 = 30см
Відповідь:
Пояснення:
1. Дуга АС (більша) = 360° - 120° = 240°.
∠ABC - вписаний; ∠ABC = 240°/2 = 120°
2. АС - діаметр кола, тому ∠ABC = 90°
3. В ΔCBD CD - діаметр кола, тому ∠CBD = 90°. ∠ABC = ∠ABD - ∠CBD ∠ABC = 120° - 90° = 30°
4. ∠ABC i ∠ADC спираються на одну дугу AC. Тому ∠ABC = ∠ADC = 40°
5. ∠ADC вписаний, тому дуга ABC = 50° * 2 = 100°.
Дуга ADC = 360° - 100° = 260°. ∠ABC = 260°/2 = 130°
6. В ΔCBD CD - діаметр кола, тому ∠CBD = 90°. ∠ABC = ∠ABD + ∠CBD ∠ABC = 30° + 90° = 120°
7. В ΔАBС АC - діаметр кола, тому ∠АBС = 90°.
8. Дуга ACB = 180° (бо це півколо). ∠CDB вписаний, тому дуга
CB = 30° * 2 = 60°. Дуга CA = 180° - 60° = 120°. ∠ABC = 120°/2 = 60°
9. В ΔDCE DC - діаметр кола, тому ∠DEC = 90°. В ΔDEO DO = EO = r. ΔDEO - рівнобедрений, отже ∠DEO = ∠EDO = 70°
∠AEC = ∠DEC - ∠DEO = 90° - 70° = 20°